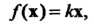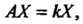10.05. Собственные векторы линейного преобразования

 

Ненулевой вектор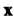Линейного пространства называется собственным вектором линейного преобразования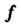Этого пространства, если существует число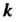Такое, что

(10.10)

Причем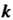- действительное число для действительного линейного пространства и комплексное число в случае комплексного пространства. Число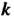Называется собственным значением вектора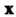Относительно преобразования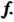Равенство (10.10) можно записать в матричном виде

(10.11)

Где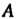- матрица преобразования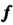В некотором базисе,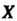-матрица-столбец из координат собственного вектора х в том же базисе. Ненулевая матрица-столбец 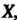удовлетворяющая уравнению (10.11), называется собственным вектором-столбцом матрицы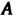С собственным значением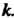

Собственные векторы и собственные значения обладают следующими свойствами.

1.  Собственный вектор линейного преобразования имеет единственное собственное значение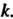

2.  Если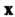- собственный вектор линейного преобразования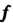С собственным числом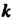И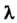- любое, отличное от нуля число, то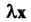- также собственный вектор преобразования/с собственным значением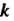

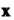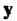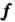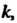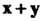3.  ЕслиИ- линейно независимые собственные векторы линейного преобразованияС одним и тем же собственным значениемТо- также собственный вектор этого преобразования с собственным значением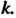

4.  Если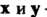- собственные векторы линейного преобразования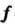С собственными числами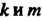, причем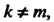То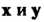Линейно независимы.

Следствие. Если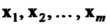— линейно независимые собственные

Векторы линейного преобразования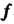С одним и тем же собственным значением 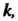то любая нетривиальная линейная комбинация этих векторов является собственным вектором этого преобразования с собственным значением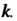

Теорема 10.3. В комплексном линейном пространстве все корни характеристического уравнения и только они являются собственными значениями линейного преобразования.

(10.13)

Координаты собственного вектора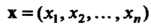Находятся из систе-

MLT l/nUDUPUUfi

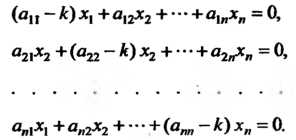
Эта система имеет ненулевое решение тогда и только тогда, когда ее определитель равен нулю (см. следствие из теоремы Крамера), т. е.

 

(10.12)

 

Это означает, что число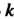Является корнем характеристического уравнения.

Замечания. 1. Уравнение (10.13) является алгебраическим уравнением п-й степени относительно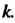Такое уравнение имеет ровно п корней, считая равные и комплексные. Среди корней этого уравнения может не оказаться действительных.

2. Собственными значениями линейного преобразования действительного пространства являются только действительные корни характеристического уравнения.

Собственные значения линейного преобразования называются также собственными значениями матрицы этого преобразования. Собственное значение называется т-краггным, если оно является m-кратным корнем характеристического уравнения.

Теорема 10.4. Корни характеристического уравнения действительной симметрической матрицы являются действительными числами.

Следствие. Действительная симметрическая матрица имеет только действительные собственные векторы.

Система (10.12) для определения координат собственного вектора в этом случае имеет только действительные решения, так как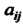И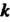- действительные числа.

Теорема 10.5. Собственные векторы действительной симметрической матрицы, соответствующие различным собственным значениям, ортогональны.

Пример 10.4. Найти действительные собственные значения и собственные векторы линейного преобразования с матрицей

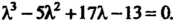
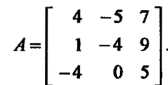
Составляем характеристическое уравнение матрицы

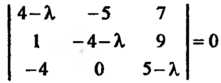
Разложим на множители многочлен в левой части уравнения:-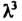

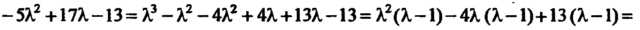
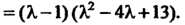Уравнение принимает вид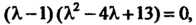Откуда

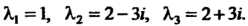Следовательно, линейное преобразование с данной матрицей имеет только одно действительное собственное значение Х = 1.

Для отыскания соответствующего собственного вектора используем систему уравнений (10.12), которая принимает вид

F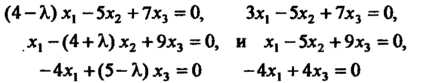

При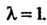Решая полученную систему, находим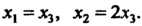Полагая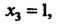

Получаем собственный вектор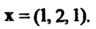

Замечание. Собственный вектор линейного преобразования определяется с точностью до произвольного множителя (см. свойство 2 собственного вектора).

< Предыдущая		Следующая >