10.04. Характеристическое уравнение линейного преобразования

 

Теорема 10.2. Если линейное преобразование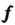В базисе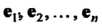Имеет

Матрицу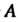И в базисе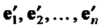- матрицу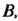То

Где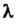— любое действительное число,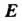— единичная матрица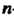-го порядка.

Отметим, что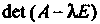Является многочленом степени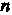Относительно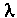И

Называется характеристическим многочленом матрицы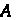Или характеристическим многочленом линейного преобразования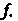

Замечание. Равенство (10.7) означает, что характеристический многочлен линейного преобразования остается неизменным при переходе к новому базису; матрица линейного преобразования меняется.

Характеристическим уравнением линейного преобразования называется уравнение

(10.8)

Где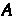— матрица этого преобразования в некотором базисе. Очевидно, характеристическое уравнение не зависит от выбора базиса. Уравнение (10.8) называют также характеристическим уравнением матрицы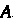, а корни уравнения - характеристическими числами линейного преобразования / или характеристическими числами матрицы..

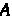Если линейное преобразование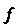В некотором базисе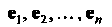Имеет

Квадратную матрицу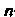-го порядка.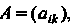, то характеристическое уравнение

(10.8) запишется так:

(10.9)

Левая часть равенства (Ю.9) является характеристическим многочленом матрицы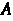; обозначим его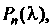Тогда характеристическое уравнение

(10.9) примет вид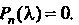

Пример 10.3. Найти характеристический многочлен и характеристические числа матрицы

В соответствии с определением характеристического многочлена получаем

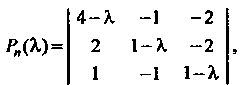
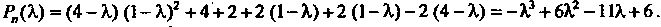
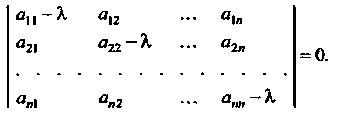
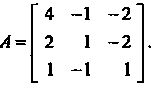
Приравнивая этот многочлен нулю, находим характеристическое уравнение 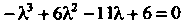Или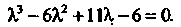Разлагая левую часть этого

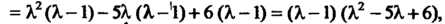Приводим данное уравнение к виду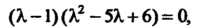Откуда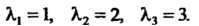Эти корни - характеристические числа данной матрицы.

< Предыдущая		Следующая >