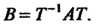10.03. Зависимость между матрицами одного и того же преобразования в различных базисах. Подобные матрицы
В и-мерном линейном пространстве фиксируем два базиса: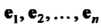
И
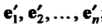; первый из них назовем старым, второй - новым. Предположим, что известно преобразование, переводящие старый базис в новый.
Теорема 10.1. Есл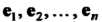и
И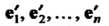
- два базиса линейного про
Странства,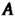
- матрица линейного преобразования в старом базисе
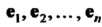то матрица
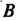Этого преобразования в новом базисе
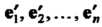Имеет вид
Где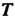
— матрица перехода от старого базиса к новому.
Следствие. Если линейное преобразование имеет невырожденную матрицу в некотором базисе, то матрица этого преобразования будет невырожденной в любом другом базисе.
Матрица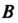
Называется подобной матрице
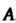, если существует невырожденная квадратная матрица
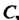Удовлетворяющая равенству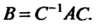
Две квадратные матрицы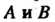
Порядка
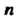Тогда и только тогда являются матрицами одного и того же линейного преобразования пространства
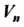В соответствующих базисах, когда матрица
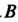Подобна матрице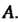
Пример 10.2. В базисе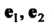
Преобразование
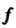Имеет матрицу
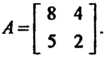
Найти матрицу преобразования
В базисе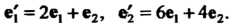
Так как
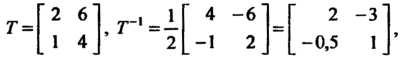
То по формуле (10.6) получаем
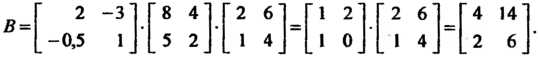
| < Предыдущая | Следующая > |
|---|
