10.02. Линейное преобразование в координатах

 

Рассмотрим линейное преобразование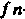-мерного линейного пространства, заданное в некотором базисе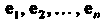Матрицей

(10.2)

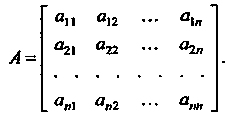
Координаты вектора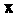И его образа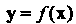Известны:

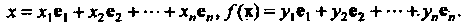(10.3)

Зависимость между координатами векторов х и у выражается формулами

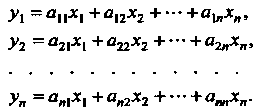
(10.4)

Формулы (10.4) можно записать в матричном ви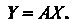де  где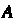Определяется формулой (10.2), а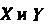-формулами

(10.5)

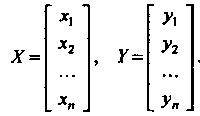
Если переменные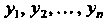Связаны с переменными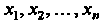Форму

Лами (10.4), то будем говорить, что задано линейное однородное преобразование переменных с матрицей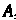, переводящее переменные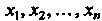В переменные

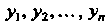. Оно обладает теми же свойствами, что и линейное преобразование 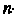-мерного линейного пространства. Линейное однородное преобразование переменных (10.4) или (10.5) называется невырожденным, если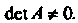

Замечание. При рассмотрении линейных преобразований (линейных операторов) пользуются и другими обозначениями. Если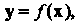Где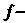

Линейное преобразование (линейный оператор) с матрицей А в некотором базисе, то пишут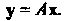Условия 1) и 2), определяющие линейное преобразование, мож

Но записать в виде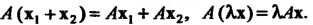

< Предыдущая		Следующая >