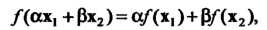10.01. Линейное преобразование и его матрица
Если указано правило,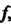
По которому каждому вектору х линейного пространства
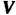Ставится в соответствие единственный вектор у этого пространства, то будем говорить, что в нем задано преобразование (отображение, оператор)
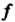Или задано преобразование пространства
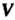В себя, и писать
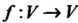. Говорят также,
Что преобразование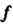
Переводит вектор
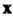В вектор
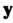, и пишут
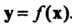. Вектор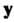
Называют образом вектора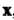
, а
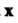- прообразом вектора
.
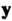Преобразование, при котором каждый вектор имеет единственный прообраз, называется взаимно однозначным (или биективным).
Преобразование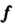
Линейного пространства
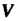Называется линейным преобразованием (линейным оператором), если для любых векторов этого пространства 
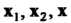И любого действительного числа
Выполняются условия
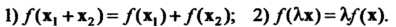
(Если рассматривается комплексное пространство, то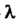
- любое комплексное число.)
Из этих условий следует, что
Где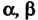
- любые числа (действительные или комплексные). Обратно, из равенства (10.1) следуют условия 1) и 2). Итак, линейное преобразование (линейный оператор) определяется равенством (10.1).
Отметим, что линейное преобразование переводит нулевой вектор в нулевой, так как, согласно условию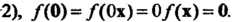
Простейшим примером линейного преобразования является тождественное преобразование или преобразование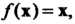
Т. е. преобразование, которое каж
Дому вектору линейного пространства ставит в соответствие тот же вектор. Линейное преобразование будет вполне определено, если заданы образы базисных векторов рассматриваемого пространства.
Пусть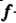
-линейное преобразование
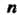-мерного линейного пространства, переводящее базисные векторы
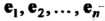В векторы
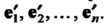Каждый из последних векторов разложим по базису:
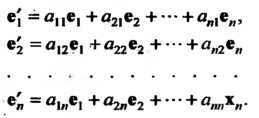
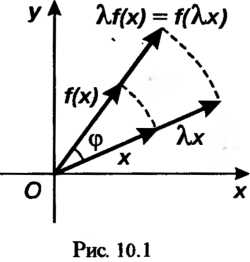
Матрица
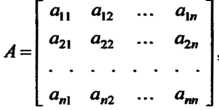
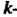
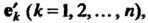
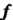
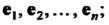
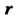
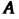
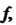
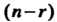
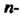
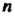
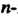
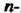
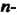
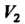
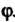
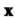
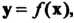
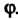
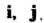
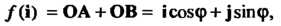
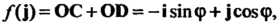
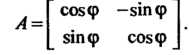
В которой к-& столбец состоит из координат вектора е* (* = 1,2,я), называется матрицей линейного преобразования / в базисе е,,е2,...,е„; ранг г матрицы А называется
Рангом преобразования /, а число (п-г) - дефектом этого преобразования. Итак, каждому линейному преобразованию л-мерного линейного пространства соответствует матрица порядка л в данном базисе; и наоборот, каждой матрице порядка л соответствует линейное преобразование п-мерного пространства.
Отметим, что матрица тождественного преобразования в любом базисе будет единичной; обратно, любой единичной матрице л-го порядка соответствует тождественное преобразование линейного л-мерного пространства.
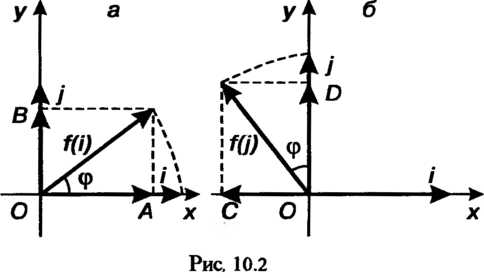
Пример 10.1. В пространстве У2 всех свободных векторов на плоскости определим преобразование поворота всех векторов вокруг начала координат на угол ф. Каждому вектору х (рис. 10.1) этой плоскости ставим в соответствие вектор у = /(х), полученный вращением вектора х на один и тот же угол ф. Это преобразование является линейным, поскольку условия 1) и 2), определяющие линейное преобразование, будут выполнены. Найдем матрицу этого линейного преобразования в базисе 1, ^, (рис. 10.2, о, б). Так как /(1) =ОА + ОВ= 1созф + ]зтф, /Ш = 0С + 00= -151ПФ +1С05ф, то
[СОЗф —51П ф 81(1 ф СОЗф
| < Предыдущая | Следующая > |
|---|
