09.8. Унитарное пространство
' Комплексное линейное пространство I/ называется унитарным пространством, если каждой паре векторов х, у е II поставлено в соответствие комплексное число, обозначаемое (х, у) и называемое скалярным произведением векторов х и у, причем выполняются следующие аксиомы: I. (х, у) = (у, х), П. (х+у, г) = (х, г)+(у, г), III. (ах, у) = а (х, у), IV. (х, х)>0 если х*0, для всех х, у, ге С/ и всех а еС (С - множества комплексных чисел).
Замечание. Черта означает комплексную сопряженность: (у, х) - комплексное число, сопряженное комплексному числу (у, х).
Из аксиом скалярного произведения в унитарном пространстве вытекают следующие свойства:
1) (х, у+г) = (х, у)+(х, г) для любых х, у, г е II;
2) (х, ау) = а (х, у) для любых х, у е V и любого а е С;
3) (0, х) = (х, 0) = О для любого х б II;
'к 1 ^ * /
Х®-*-’ =ХХа<м^,)-
I 7=1 ) 1=1 7=1
Примером унитарного пространства является множество С„ упорядоченных систем и комплексных чисел
Х "" (^1) ®2.....)> У = (Р1 >р2»"->Ря)»*'ч
Для которых скалярное произведение определено формулой (х, у) = а, р, + а2р2 + ¦ - + аД,,
Где Р* - комплексное число, сопряженное числу Р* {к = 1,2,..., п).
Унитарным преобразованием комплексного линейного пространства называется линейное преобразование, сохраняющее положительно определенную эрмитову форму дс, Х| +х2х2 н-----где х,,х2, ...,х„- координаты вектора пространства В ортонормированием базисе относительно эрмитова произведения, задаваемого этой формой, унитарное преобразование записывается унитарной матрицей. (Унитарной матрицей называется квадратная невырожденная матрица А, удовлетворяющая условию А~'=АТ, где А~' - обратная матрица, Ат - транспонированная и комплексно-сопряженная матрица Определитель унитарной матрицы по модулю равен единице. Все характеристические корни унитарной матрицы по модулю равны единицы. Всякая (действительная) ортогональная матрица есть в то же время унитарная матрица
6 Зак. 1
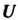
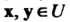
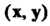
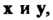
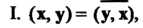
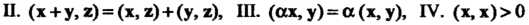
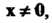
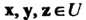
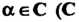
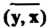
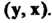
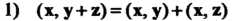
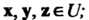
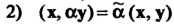

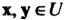
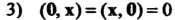
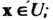
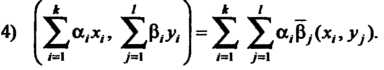
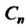
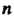
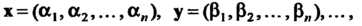
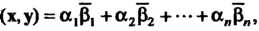
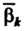
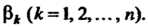
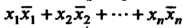
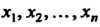
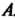
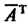
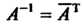
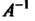
161
ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ (ЛИНЕЙНЫЕ ОПЕРАТОРЫ)
| < Предыдущая | Следующая > |
|---|