09.7. Евклидово пространство
Определение евклидова пространства. В линейном действительном пространстве V, кроме операций сложения векторов и умножения вектора на действительное число, введем еще одну операцию, которую назовем скалярным умножением векторов. Каждой упорядоченной паре векторов х, у е V поставим в соответствие действительное число, которое назовем их скалярным произведением и обозначим (х, у). Потребуем, чтобы для любых х, у, г 6 V и любого числа а е К выполнялись следующие аксиомы: I. (х, у) = (у, х), II. (х + у, г) = = (х, г) + (у, г), III. (ах, у) = а(х, у), IV. (х, х)>0 для всех х*0, (х, х) = 0 для х = 0.
Очевидно, скалярное произведение равно нулю, если хотя бы один из векторов нулевой: (0, у) = (Ох, у) = 0 (х, у) = 0.
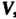
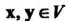
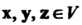
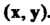
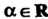
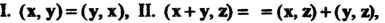
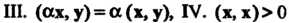
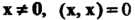
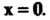
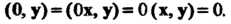
Скалярное произведение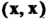
Вектора
На себя называется скалярным квад
Ратом этого вектора и обозначается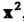
, т. е.
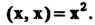(9.14)
Евклидовым пространством называется линейное действительное пространство, в кагором задана операция скалярного умножения векторов, удовлетворяющая аксиомам I — ГУ. Если и-мерное линейное пространство является евклидовым, то будем называть его евклидовым n-мерным пространством, а базис этого линейного пространства - базисом евклидова Пространства.
Примеры евклидовых пространств. 1.хВ линейном пространстве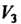
Скалярное произведение двух векторов
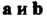Определим так, как в п. 3.6; аксиомы
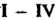для него будут выполнены (см. свойства скалярного произведения и определение скалярного квадрата вектора).
Следовательно, линейное пространство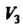
Всех свободных векторов с обычным определением скалярного произведения является евклидовым пространством.
2. Рассмотрим л-мерное линейное пространство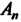
Упорядоченных совокупностей п действительных чисел. Скалярное произведение двух его элементов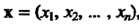
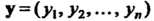По аналогии с формулой (3.21) определим соотношением
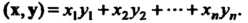(9.15)
Легко видеть, что все аксиомы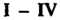
Скалярного произведения при этом вы
Полняются. Таким образом, рассматриваемое линейное пространство со скалярным произведением (9.15) является евклидовым пространством, его обозначают Е„.
3. В бесконечномерном линейном пространстве
Всех функций, непрерывных на отрезке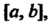
Скалярное произведение двух его функций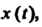
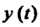Определим формулой
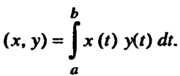(9.16)
Непосредственной проверкой можно убедится в том, что аксиомы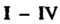
Скаляр
Ного произведения будут выполнены, в частност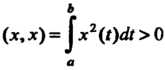и
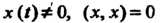При
При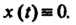
Следовательно, линейное пространство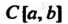
С указанным определением скаляр
Ного произведения любых двух его элементов является евклидовым пространством.
Норма вектора евклидова пространства. Нормой вектора евклидова пространства называется арифметическое значение корня из скалярного квадрата этого вектора. Норму вектора х обозначим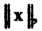
Тогда по определению
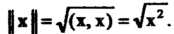(9. П)
Норма вектора обладает следующими свойствами: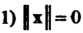
Тогда и только тогда, когда
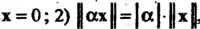, где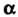
- действительное число;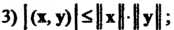
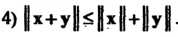
Неравенством Коши - Буняковского называют неравенство
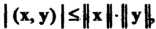(9.18)
А неравенством треугольника - неравенство
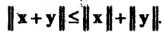(9-19)
Запишем норму и неравенства (9.18), (9.19) для векторов (элементов) каждого из рассмотренных выше евклидовых пространств.
В евклидовом пространстве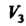
С обычным определением скалярного произведения норма вектора совпадает с его длиной, т. е.
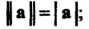Это следует из формул
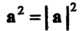И (9.17). Неравенства (9.18) и (9.19) принимают соответственно вид 
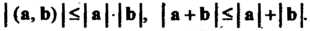Отметим, что неравенство
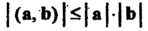следует из формулы (3.18). Неравенство
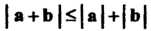Следует из определений
Суммы векторов и длины вектора; оно имеет простой геометрический смысл (в треугольнике сумма длин двух сторон больше длины третьей стороны).
В евклидовом пространстве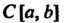
Норма элемента
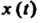Определяется формулой
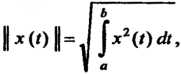
Неравенства (9.18) и (9.19) принимают вид
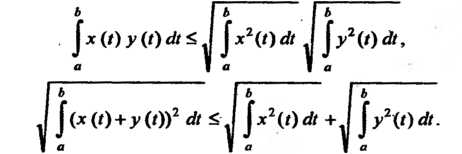
В евклидовом пространстве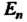
Со скалярным произведением (9.15) норма элемента
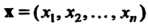Определяется формулой
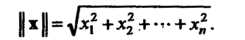
А неравенства (9.18) и (9.19) принимают вид
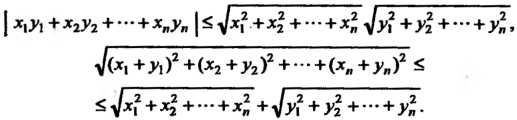
Со5ф = 71 п м й (0$ф<2л). (9.20)
Угол между двумя векторамн евклидова пространства. Углом между, двумя векторами х и у евклидова пространства называется угол ф, для которого
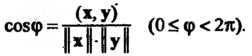
Отметим, что в пространстве У3 всех свободных векторов введенное понятие угла совпадает с понятием угла, рассматриваемого в векторной алгебре.
Два вектора евклидова пространства называются ортогональными, если их скалярное произведение равно нулю. Очевидно, ну^юй вектор ортогонален любому другому вектору. В пространстве У3 ортогональность векторов означает их перпендикулярность.
Из определений следует, что ненулевые векторы х и у ортогональны тогда и только тогда, когда созф = 0!
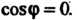
Равенство
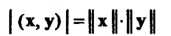
|(х, У)| = 1х|||у| (9.21)
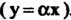
Выполняется тогда и только тогда, когда х и у коллинеарны (у = ах ). Друшми словами, в формуле (9.18) равенство достигается лишь в случае коллинеарности векторов х и у.
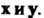
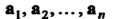
Ортонормироваиный базис. Система векторов а,,а2,...,а„ называется ортогональной, если эти векторы ортогональны, т. е. (а,,а4) = 0 при гФк.
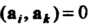
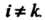
Теорема 9.7. Ортогональная система ненулевых векторов линейно независима.
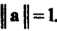
Вектор а называется нормированным или единичным, если Ц а II = 1. Если а ненулевой вектор, то каждый го векторов
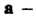
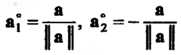
Х Я1 = Й |Г> Я2 ~ ~ й п (9.22)
Будет нормированным. Нахождение для данного вектора нормированного вектора по формулам (9.22) называется нормированием данного вектора, а множитель р = \/± | а | - нормирующим множителем.
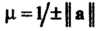
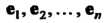
Система векторов е,, е2,..., е„ называется ортонормированной, если она ортогональна и каждый вектор является нормированным, т. е.
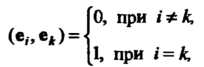
ГО, при I* к,
(е„е*Н (9.23)
[1, при 1 = к,
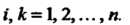
Где I, & = 1,2,...,и.
Базис п-мерного евклидова пространства называется ортонормированным, если базисные векторы образуют ортонормированную систему.
Теорема 9.8. Во всяком евклидовом п-мерном пространстве (п > 2) существует ортонормироваиный базис.
Выражение скалярного произведения через координаты векторов в ортонормированием базнсе. Пусть в п-мерном евклидовом пространстве фиксирован ортонормироваиный базис е,, е2,..., е„ и даны векторы этого пространства
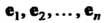
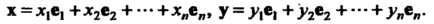
Х = х, е, +х2е2 н— +*„е„, у = >,е, +>2е2 + —+у„е„. (9.24)
Скалярное произведение этих векторов выражается формулой
{х, у) = х1у1+х2у2+-- + 'хпу„. (9.25)
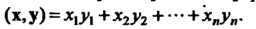
Отсюда следует, что
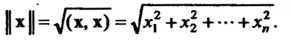
| < Предыдущая | Следующая > |
|---|
