09.6. Преобразование координат вектора при изменении базиса
В линейном л-мерном пространстве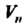 Фиксируем два базиса
Фиксируем два базиса
(9.8)
 (9.9)
(9.9)
Матрицей перехода от базиса (9.8) к базису (9.9) называется матрица системы векторов (9.9) в базисе (9.8). Каждый вектор системы (9.9) можно разложить по базису (9.8). Пусть
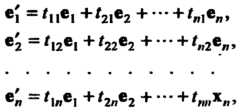 (9.10)
(9.10)
Тогда матрица перехода от базиса (9.8) к базису (9.9) имеет вид
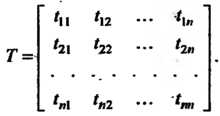
(9.11)
Матрица перехода от одного базиса к другому невырожденная (так как базисные векторы линейно независимы). Всякую невырожденную матрицу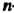 -го порядка можно рассматривать как матрицу перехода от одного базиса
-го порядка можно рассматривать как матрицу перехода от одного базиса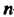 -мерного линейного пространства к другому базису этого пространства. Очевидно, матрица
-мерного линейного пространства к другому базису этого пространства. Очевидно, матрица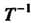 обратная матрице (9.11), является матрицей перехода от базиса (9.9) к базису (9.8).
обратная матрице (9.11), является матрицей перехода от базиса (9.9) к базису (9.8).

Теорема 9.6. Если х1гх2,...,х„ - координаты вектора х в базисе е„е2,...,е„; Х1,Х2,...,х' - координаты того же вектора в базисе е{,е'2,...,е’„,то
X = ТХ\ (9.12)
Где
(9.13)
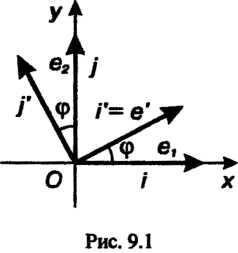
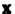
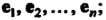
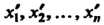
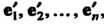
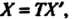
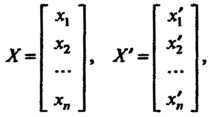
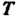
Т — матрица, определяемая формулой (9.1!).
Замечание. Теорема 9.6 выражает старые координаты хх, хг, ...,х„ вектора х через его новые координаты. Чтобы получить формулы, выражающие новые координаты через старые, умножим слева равенство (9.12) на матрицу Г-1, обратную матрице Т, получим Т~хХ = Т~хТХ', Т~'Х = X’ или Х‘ = Т~*Х.
Пример 9.4. В пространстве У2 рассмотрим базис е, =«, е2 = где I, } - орты, и базис е[ = Г, е’2 = где Г, У - орты, причем Г образует с 1 угол <р (рис.9.1). В данном случае |' = 1со$ф+|$п]ф, * ], = -15тф + |со5ф. Матрица перехода от базиса 1,,} к базису V, У имеет вид
Г С08ф -51Пф 1
[ 51Пф С05ф ]
Если вектор а имеет координаты х, у в базисе I, ^ х\ у - в базисе Г,|', то
Х = .х'с05ф-у'$тф, у = У 51П ф + у' С05ф.
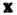
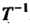
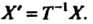
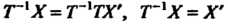
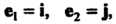
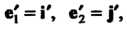
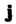
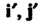
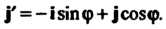
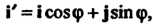
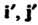
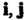
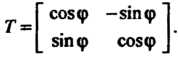
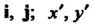
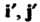
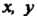
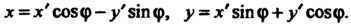
| < Предыдущая | Следующая > |
|---|