09.5. Ранг системы векторов линейного пространства

 

Рассмотрим систему т векторов

А1 = («И» «21>> вш)

®2 = («12> «22»-"> «л2)

(9.6)

 

®|я («11я» «2л», » «ит)

Линейного л-мерного пространства, координаты которых заданы в одном и том же базисе. Системе векторов (9.6) поставим в соответствие матрицу

 

(9.7)

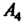
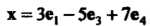
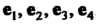
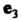
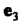
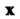
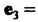
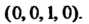
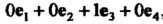
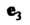
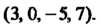
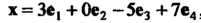
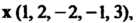
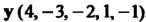
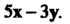
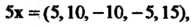
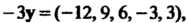
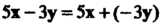
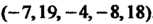
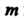
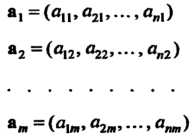
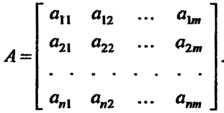
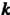
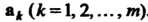
В к-м столбце которой записаны координаты вектора лк(к = \,2,...,т). Матрицу

(9.7)  называют матрицей системы векторов (9.6) в данном базисе, а ранг этой матрицы — рангом системы векторов а,,а2,..., я„. Обратно, если дана матрица

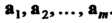
(9.7),  то ей можно поставить в соответствие систему (9.6) т векторов линейного я-мерного пространства Согласно свойству 5 п. 9.4, будем говорить, что столбцы матрицы (9.7) линейно зависимы, если векторы (9.6) линейно зависимы и обратно.

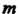
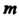
Теорема 9.4. Для того чтобы т векторов п-мерного линейного пространства были линейно независимы, необходимо и достаточно,- чтобы ранг матрицы этой системы был равен т.

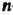
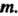
Следствие 1. Система п векторов п-мерного линейного пространства линейно независима тогда и только тогда, когда матрица этой системы векторов является невырожденной.

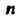
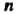
Следствие 2. Если ранг матрицы системы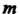Векторов линейного пространства равен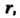То максимальное число линейно независимых векторов этой системы равно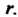

Пример 9,3. Найти максимальное число линейно независимых векторов в системе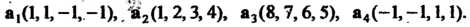

Матрица данной системы векторов имеет вид

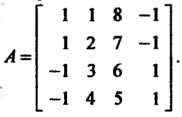
Так как ранг этой матрицы равен 3 (см. пример 5.16), то максимальное число линейно независимых векторов этой системы равно 3.

Теорема 9.5. Максимальное число линейно независимых строк всякой матрицы равно максимальному числу ее линейно независимых столбцов, т. е. равно рангу этой матрицы.

< Предыдущая		Следующая >