09.4. Координаты вектора линейного пространства
Теорема 9.3. Если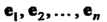
- базис линейного п-мерного пространст
Ва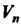
, то любой вектор
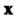Этого пространства линейно выражается через базисные векторы
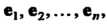Т.
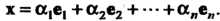/ (9.5)
Коэффициенты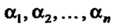
Этого разложения определяются. однозначно.
Выражение (9.S) называется разложением вектора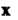
По базису
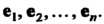Координатами вектора
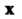В базисе
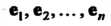Называют коэффициенты
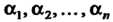В разложении этого вектора по данному базису, т. е. в формуле (9.5). Если вектор х в некотором базисе имеет координаты
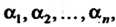То пи
Шут
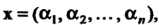Или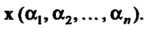
Операции над векторами сводятся к операциям над их координатами на основании следующих свойств.
1. Вектор является нулевым вектором линейного пространства тогда и только тогда, когда все его координаты в любом базисе равны нулю.
2. Координаты суммы двух векторов в некотором базисе равны сумме соответствующих координат данных векторов в том же базисе.
3. Координаты произведения вектора на число равны произведению соответствующих координат на это число (в одном и том же базисе).
4. Два вектора равны тогда и только тогда, когда равны их соответствующие координаты в одном и том же базисе.
5. Вектор у является линейной комбинацией векторов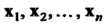
Тогда и
Только тогда, когда каждая координата вектора у является такой же линейной комбинацией соответствующих координат этих векторов в одном и том же базисе.
Пример 9.1. Пусть Д, - четырехмерное линейное пространство с базисом е1>е2,е3,е4. Найти координаты векторов е3 и х = Зе, — 5е3 + 7е4 в этом базисе.
Представим каждый из векторов е3 и х в виде (9.5). Так как = Ое, + 0е2 + 1е3 +0е4, то. вектор % имеет координаты (0,0,1,0). Поскольку х = Зе, + 0е2 - 5е3 + 7е4, то вектор х имеет координаты (3,0, - 5,7).
Пример 9.2. В некотором базисе даны векторы х(1,2,-2,-1,3), у (4,-3,-2,1,-1). Найти координаты вектора 5х-3у.
Так как 5х =(5,10,-10,-5,15), -3у = (-12,9,6,-3,3), то вектор 5х - Зу = 5х + (- Зу) имеет координаты (- 7,19, - 4, - 8,18).
| < Предыдущая | Следующая > |
|---|
