09.3. Размерность и базис линейного пространства. Изоморфизм линейных пространств

 

Число п называется размерностью линейного пространства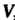, если выполняются следующие условия: 1) в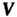Существует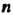Линейно независимых векторов; 2) любая система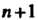Векторов из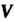Линейно зависима. Размерность линейного пространства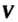Обозначают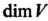(от французского слова-

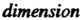Размерность). Если пространство состоит из одного нулевого элемента, то его размерность считают равной нулю. Размерность линейного пространства - это наибольшее возможное количество линейно независимых элементов в нем. Понятие размерности согласуется с наглядным представлением о ней; так, пространство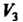Всех свободных векторов является трехмерным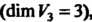, пространство 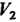— двумерным, пространство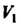- одномерным.

Базисом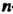-мерного линейного пространства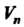Называется любая упорядоченная система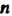Линейно независимых векторов этого пространства. Приведем примеры базисов некоторых линейных пространств. Базис пространства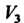Образует любая тройка некомпланарных векторов, так как эти векторы линейно независимы (см. теорему 3.4), и любая четверка векторов линейно зависима (см. теорему 3.6). Базис пространства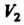Образует два любых неколлинеарных вектора, поскольку они

Линейно независимы (см. теорему 3:2), и любой вектор плоскости, определяемой двумя векторами, можно разложить по ним (см. терему 3.3). Базисом линейного пространства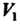Является любой ненулевой вектор, коллинеарный данной прямой.

Линейное пространство, в котором имеется базис, состоящий из конечного числа векторов, называется конечномерным. Примерами конечномерных пространств являются пространства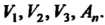

Линейное пространство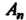Является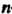-мерным, а его базис образует система векторов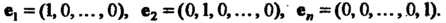

Линейное пространство называется бесконечномерным, если при любом натуральном числе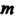В нем найдется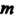Линейно независимых векторов. Примером бесконечномерного пространства может служить линейное пространство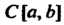Всех функций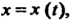Определенных и непрерывных на отрезке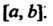

Два линейных пространства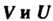Называются изоморфными, когда между их элементами можно установить взаимно однозначное соответствие такое, что если 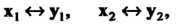ГдеТо

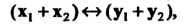
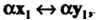Где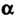- действительное число.

Теорема 9.2. Два линейных пространства изоморфны тогда и только тогда, когда они имеют одинаковую размерность.

В частности, пространство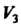(всех свободных векторов) и пространство 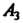(всех упорядоченных троек действительных чисел) изоморфны. Отметим также, что каждое конечномерное линейное пространство размерности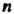Изоморфно линейному пространству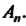

< Предыдущая		Следующая >