09.2. Линейная зависимость и линейная независимость векторов линейного пространства
Рассмотрим векторы (элементы) х,, х2,..., х„ линейного пространства. Вектор
У = а, х, +а2х2 + -+а„х„, где а„а2.....а„ - некоторые числа, называется
Линейной комбинацией векторов х„х2,...,х„, а числа а„а2.....а„ -
Коэффициентами этой линейной комбинации. Если все числа а, (/ = 1,2,..., л) равны нулю, то линейная комбинация называется тривиальной. Если хотя бы одно из чисел а, отлично от нуля, линейная комбинация называется нетривиальной.
Система векторов
Называется линейно зависимой, если существуют числа
Не все равные нулю, такие, что
Если таких чисел не существует, т. е. равенство (9.3) выполняется только в случае
То система векторов (9.1) называется линейно независимой.
Другими словами, векторы (9.1) называются линейно зависимыми, если существует их нетривиальная линейная комбинация, равная нуль-вектору, и линейно независимыми, если только их тривиальная линейная комбинация является нуль-вектором.
Из. определения линейной зависимости и линейной независимости векторов вытекают следующие утверждения.
1. Всякая система векторов, содержащая нуль-вектор, является линейно зависимой.
2. Если к(к<п) векторов системы (9.1) линейно зависимы, то и вся система линейно зависима.
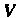
3. Если из системы линейно независимых векторов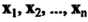 Отбросить
Отбросить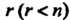 векторов, то оставшиеся векторы образуют также линейно независимую систему.
векторов, то оставшиеся векторы образуют также линейно независимую систему.
4. Если среди векторов системы (9.1) имеются такие векторы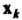 И
И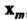 , что
, что
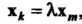 , где
, где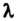 - некоторое число, то система (9.1) линейно зависима.
- некоторое число, то система (9.1) линейно зависима.
Теорема 9.1. Векторы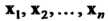 Линейно зависимы тогда и только то
Линейно зависимы тогда и только то
Гда, когда хотя бы один из них является линейной комбинацией всех остальных.
Эта теорема выражает необходимое и достаточное условие линейной зависимости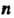 Векторов
Векторов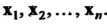
Два вектора линейного пространства называются коллинеарными, если они линейно зависимы, и неколлинеарными, если они линейно независимы. Три вектора линейного пространства называются компланарными, если они линейно зависимы, и некомпланарными, если они линейно независимы. Введенные понятия коллинеарности и компланарности векторов линейного пространства совпадают с известными из аналитической геометрии понятиями коллинеарности и компланарности обычных векторов.
| < Предыдущая | Следующая > |
|---|