09.1. Линейное пространство. Подпространство
Линейным действительным пространством или векторным действительным пространством называется множество Vэлементов х, у, ж, для которых определены операции сложения элементов и умножения элемента на действительное число, удовлетворяющие следующим аксиомам: I. х + у = х + у, II. (х+у)+2=х+(у+-ж), III. Существует нулевой элемент 0 такой, что х+0 = х, IV. Для каждого х еУ существует противоположный элемент - х такой, что х + (-х) = О, V. 1х = х, VI. а(рх)= (ар)х, VII. а(х + у) = =ах+ау, VIII. (а+р)х = ах+рх.
Эти аксиомы выполняются соответственно для всех х, у, г е V, а, р е*К.
Элементы действительного линейного пространства называются векторами. Замечание. Аналогично определяется комплексное линейное пространство: вместо множества К действительных чисел рассматривается множестве С комплексных чисел.
Из определения линейного пространства вытекают следующие утверждения.
1. В линейном пространстве имеется единственный нулевой элемент.
2. Для любого элемента х линейного пространства существует единственны элемент - х.
3. Для элемента - х противоположным будет элемент х.
4. Для любого элементах произведение Ох = 0, где 0 - нуль, 0 - нулевой элемен
5. Для любого элемента х (-1) х = - х, где (- х) - элемент, противоположный*
6. Для любого числа а произведение аО = 0, где 0 - нулевой элемент.
7. Если ах = 0 и а * 0, то х = 0.
8. Если ах = 0 и х * 0, то а = 0.
Равенство ах = 0 выполняется тогда и только тогда, когда а = 0 или х = 0. Замечание. Сумму х+(-у) обозначают х - у и называют разноси
Элементов х и у.
Примеры линейных пространств.
1. Множество У3 всех свободных векторов а (о,, а2> а3), для которых оп]
Делены сложение и умножение вектора на число так, как в п. 3.2, является ли» ным пространством. Отметим, что роль нулевого элемента здесь играет ну вектор; для любого вектора а противоположным является - а. Аксиомы I - \ выполняются, о чем свидетельствуют формулы п. 3.2.
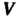
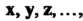
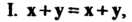
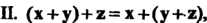
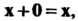
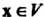
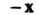
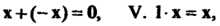
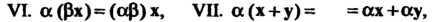
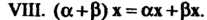
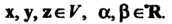
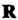
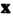
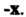
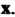
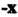
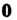
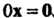
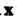
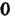
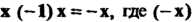
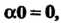
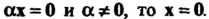
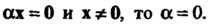
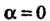
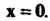
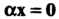
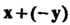
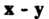
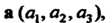
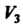
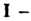
2. Множество всех матриц размером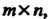 Для которых определены сложение матриц и умножение матрицы на число соответственно формулами (S.2), (S.4). Роль нулевого элемента здесь играет нулевая матрица; для матрицы
Для которых определены сложение матриц и умножение матрицы на число соответственно формулами (S.2), (S.4). Роль нулевого элемента здесь играет нулевая матрица; для матрицы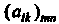 Противоположной является матрица
Противоположной является матрица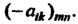 Аксиомы
Аксиомы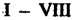 Выполняются (см. п. 5.2, свойства 1-8 линейных операций над матрицами).
Выполняются (см. п. 5.2, свойства 1-8 линейных операций над матрицами).
3. Множество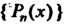 Всех алгебраических многочленов степени, не превышающей натурального числа
Всех алгебраических многочленов степени, не превышающей натурального числа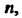 Для которых операции сложения многочленов и умножения многочлена на действительное число определены обычными правилами. Нулевой элемент - многочлен, все коэффициенты которого равны нулю; для многочлена
Для которых операции сложения многочленов и умножения многочлена на действительное число определены обычными правилами. Нулевой элемент - многочлен, все коэффициенты которого равны нулю; для многочлена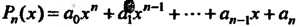 Противоположным будет
Противоположным будет
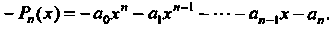
Замечание. Множество всех многочленов степени, точно равной натуральному числу и, не является линейным пространством, так как сумма двух таких многочленов может оказаться многочленом степени ниже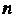 (т. е. не принадлежать рассматриваемому множеству).
(т. е. не принадлежать рассматриваемому множеству).
4. Множество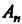 Элементами которого являются упорядоченные совокупности и действительных чисел
Элементами которого являются упорядоченные совокупности и действительных чисел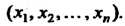 Каждый элемент этого множества будем обозначать одним символом, например
Каждый элемент этого множества будем обозначать одним символом, например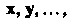 И писать
И писать
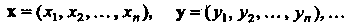 Действительные числа
Действительные числа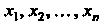 называют координатами элемента х. Линейные операции над элементами
называют координатами элемента х. Линейные операции над элементами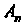 Определяются формулами
Определяются формулами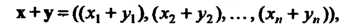
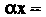
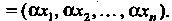 Отметим, что элемент
Отметим, что элемент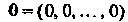 Является нулевым,
Является нулевым,
Элемент _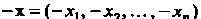 __ - противоположным элементу
__ - противоположным элементу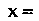
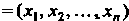
5. Множество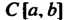 Всех функций
Всех функций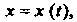 Определенных и непрерывных на отрезке
Определенных и непрерывных на отрезке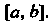 Операции сложения этих функций и умножения функции на число определяются обычными правилами. Нулевым элементом является функция
Операции сложения этих функций и умножения функции на число определяются обычными правилами. Нулевым элементом является функция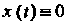 Для всех
Для всех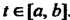 . Элементом, противоположным
. Элементом, противоположным
Ъ
Элементу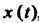 , будет
, будет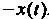
Множество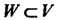 Называется подпространством линейного пространства
Называется подпространством линейного пространства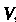 ,
,
Если выполняются следующие условия: 1. В множестве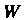 Определены те же операции, что и в множестве
Определены те же операции, что и в множестве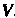 . 2. Если _
. 2. Если _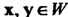 , то
, то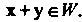 3. Если
3. Если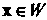 , то
, то 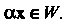 . Очевидно, всякое подпространство
. Очевидно, всякое подпространство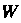 Линейного пространства
Линейного пространства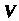 Является линейным пространством, т. е. в
Является линейным пространством, т. е. в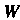 Выполняются аксиомы
Выполняются аксиомы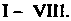 Прежде всего, в
Прежде всего, в
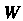 Имеется нулевой элемент
Имеется нулевой элемент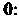 Если
Если ,' то
,' то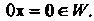 Для любого элемента
Для любого элемента
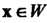 Имеется противоположный элемент
Имеется противоположный элемент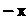 : если
: если То
То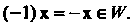
Отметим, что нулевой элемент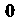 Линейного пространства
Линейного пространства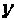 Образует подпространство этого пространства, которое, называют нулевым подпространством.
Образует подпространство этого пространства, которое, называют нулевым подпространством.
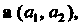

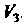
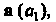
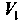
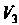
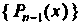
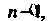
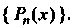
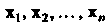
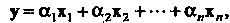
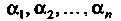
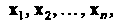
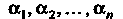
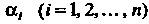
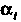
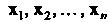
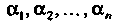
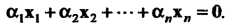
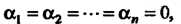
Само линейное пространство V можно рассматривать как подпространство, этого пространства. Эти подпространства называются тривиальными, а все другие, если они имеются, - нетривиальными. Приведем примеры нетривиальных подпространств. 1. Множество У2 всех свободных векторов а (о,, а2), параллельных
Некоторой плоскости, для которых обычным образом определены операции сложения векторов и умножения вектора на число, представляет подпространство линейного пространства У3. 2. Множество У, всех свободных векторов а (в,), параллельных некоторой прямой, также является подпространством линейного пространства У3. 3. Множество { Р„_,(*)} всех алгебраических многочленов степени, не превышающей натурального числа и —41, является подпространством линейного пространства {Р„(х) }.
| < Предыдущая | Следующая > |
|---|