08.7. Разложение дробной рациональной функции в сумму элементарных дробей
Целой рациональной функцией называют алгебраический многочлен. Дробной рациональной функцией или рациональной дробью называется отношение двух многочленов:
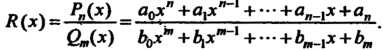(8.26)
Если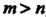
, то рациональная дробь называется правильной.
Элементарными дробями называются рациональные дроби вила
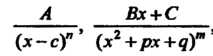
Где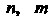
- натуральные числа;
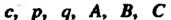- действительные числа;
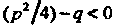(корни трехчлена
Являются комплексными).
Всякую правильную рациональную дробь можно разложить в сумму элементарных дробей на основании следующей теоремы.
Теорема 8.5. Если дана правильная рациональная дробь (8.26) и
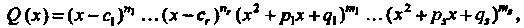
Где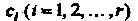
- попарно различные действительные корни многочлена
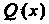Кратности
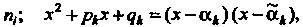Где
И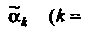
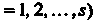- попарно различные при разных к корни многочлена
Кратно
Сти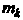
, то существуют действительные числа
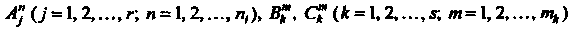
Такие, что
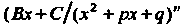
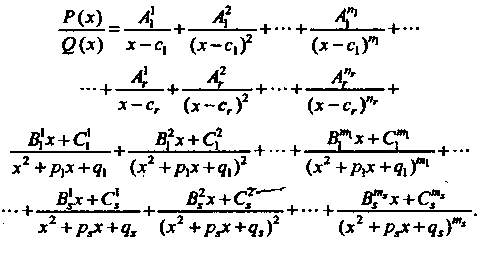
Отметим, что каждому действительному корню с кратности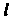
Соответствует сумма
Элементарных дробей вида
А каждой паре комплексно-сопряженных корне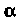й
И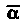
(таких, что
Кратности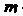
- сумма дробей вида
Пример 8.18. Разложить в сумму элементарных дробей рациональную
Дробь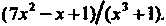
Так как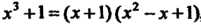
, то искомое разложение имеет вид
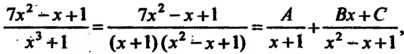
Где коэффициенты А, В, С пока не определены. ,
Приводя к общему знаменателю правую часть и сравнивая коэффициенты при одинаковых степенях х, получаем
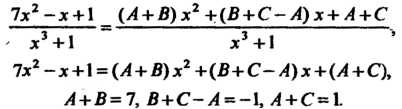
Из этой системы уравнений находим
Следовательно,
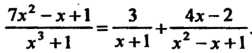
Пример 8.19. Разложить в сумму элементарных дробей рациональную
Дробь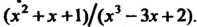
Разлагая знаменатель на множители, получаем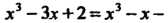
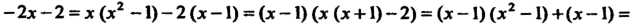
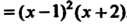Данную рациональную дробь представим в виде суммы элементарных дробей 
откуда
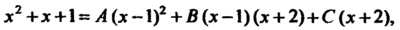
Сравнивая коэффициенты при одинаковых степенях, получаем уравнения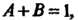
Из которых находим
Следовательно, разложение (I) примет вид
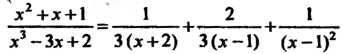
Замечание. Коэффициенты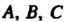
Разложения (I) можно получить и другим способом. Полагая в тождестве (II)
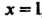, получаем
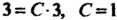. Положив в этом тождестве
, получим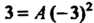
, откуда
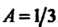. Аналогично при
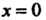Находим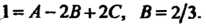
Глава 9
ЛИНЕЙНЫЕ ПРОСТРАНСТВА
| < Предыдущая | Следующая > |
|---|
