08.4. Кубические уравнения
Кубическим называется уравнение
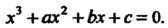
Х3 +ах2 +Ьх+с = 0. (8.14)
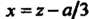
Это уравнение с помощью формулы х =2-а/3 можно привести к виду

Г3+рг+д = 0. (8.15)
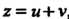
Корни кубического уравнения (8.15) вычисляются по формуле г = и+V, где
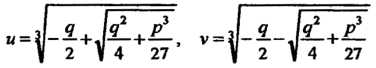
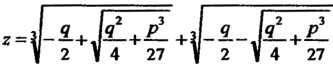



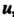
Г = ]1--+л&-+— +]!---]—+— (8.17)
|| 2 | 4 27 1 2 н 27
Все три корня уравнения (8.15) определяются следующими формулами:
Г, = и, + V,, г2 = це + у, е2, 23 = и, е2 +у, е, (8.18)
Где и, - любое из трех значений и, определяемых первой из формул (8.16), V, -
То из трех значений V, которое соответствует и, на основании равенства



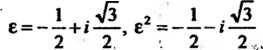
- кубические корни из единицы.
Дискриминантом уравнения (8.15) называется выражение

Уравнение (8.15) при Г><0 имеет один действительный и два комплексно-сопряженных корня: при й = 0 - три действительных корня, причем два равных; при X) > 0 - три различных действительных корня.
Замечание. Третий случай (Х>>0) называется неприводимым. В этом случае все корни уравнения (8.15) с действительными коэффициентами являются действительными, однако для нахождения их по формуле (8.17) следует извлекать кубические корни из комплексных чисел.
Формула (8.17) называется формулой Кардано. Правило, соответствующее этой формуле, впервые опубликовано в книге итальянского ученого Д. Кардано «Великое искусство или о правилах алгебры» (1545). Это правило решения кубического уравнения было получено ранее (1535) другим итальянским математиком Н. Тартальей.
Пример 8.10. Решить уравнение г3-6г + 9 = 0. Это уравнение вида (8.15), для которого р = - 6, д = 9. Составим выражение
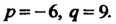
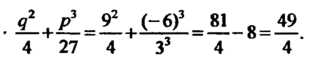

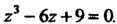
По формулам (8.16) находим и и у:

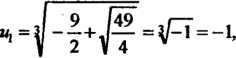
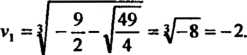
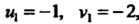
Следовательно, и, =-1, V, = - 2, равенство (8.19) выполняется. По формулам
(8.18) с учетом формул (8.20) находим
2, =«,+у, =-3,
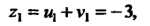

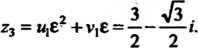
Замечание. Корни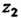 И
И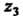 Можно найти и другим способом. Так как
Можно найти и другим способом. Так как 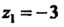 - корень уравнения, то многочлен
- корень уравнения, то многочлен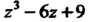 Делится на
Делится на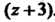 . Произ
. Произ
Ведя это деление, получим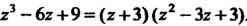 . Данное уравнение при
. Данное уравнение при
Мет вид . откуда
. откуда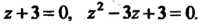 Последнее зрав-
Последнее зрав-
Нение имеет корни

Пример 8.11. Решит уравнение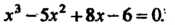 Разложим на множители многочлен в левой части уравнения:
Разложим на множители многочлен в левой части уравнения:

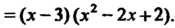 Данное уравнение примет вид
Данное уравнение примет вид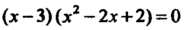 И
И
Распадается на два уравнения: Которые имеют корни
Которые имеют корни
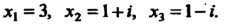
| < Предыдущая | Следующая > |
|---|