08.3. Квадратные уравнения
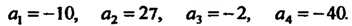
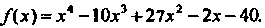

Алгебраическим уравнением л-й степени с одной переменной х называется уравнение вида
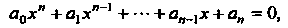
(8.9)
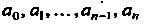
Где о0, о,,... ,о„_1, а„ — заданные числа, называемые коэффициентами.
Корнем алгебраического уравнения (8.9) называется такое значение переменной х = с, при котором оно обращается в тождество, т. е. а0с" + + о1ся_| + - о„_1с+о„ = 0.
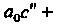
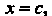
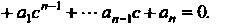
Выражение «решить уравнение» означает найти все его корни.
Квадратным называется уравнение вида

Ах2+Ьх+с = 0 (аФ 0). Корни уравнения (8.10) вычисляются по формуле
(8.10)
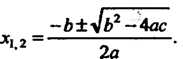
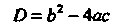

Бели а, Ъ, с - действительные числа, то квадратное уравнение (8.10) при О > 0 имеет два различных действительных корня, при I)=0 - два равных действительных корня, при Б <0 - два комплексно-сопряженных корня.
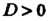


Отметим, что коэффициенты квадратного уравнения (8.10) могут быть и комплексными числами. Его корни также вычисляются по формулам (8..11). В этом случае дискриминант будет комплексным числом.
Уравнение (8.10) можно привести к виду

Корни этого уравнения вычисляются по формуле
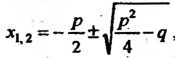
Которая является частным случаем формулы (8.11).
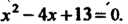
Пример 8.8. Решить уравнение х2-4х+13=0.

По формуле (8.13) получаем х, 2 = 2±>/4-13 = 2 ±./-9. Это уравнение имеет
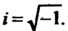
Корни х, = 2 + 3«, х2 =2-3», где «= ^-Т.
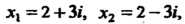
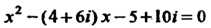
Пример 8.9. Решить уравнение х2 -(4+6/)х-5 + 10»'= 0 с комплекс-, ными коэффициентами.

По формуле (8.13) находим х12 = (2 + 30±д/(2+3/)2 -(-5+100 = = (2 + 31)±л/4+12»+9/2+5-10» =(2+3|)±-Л7 = (2 + 3*)±(1 + /); х,=3+4/,х2=1+2».
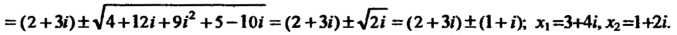
| < Предыдущая | Следующая > |
|---|