08.2. Корни многочлена. Теорема Безу

 

Значением многочлена

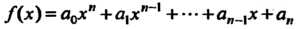(8.3)

При х = с называется число

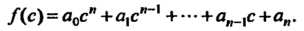
Число с называется корнем многочлена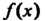Или корнем уравнения 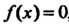если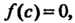Т. е.

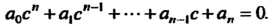
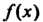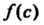Теорема 8.2. (Безу). Остаток г от деления многочленаНа линейный многочленРавен значениюМногочлена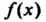При, т. е.

(8.4)

Следствие. Число с тогда и только тогда будет корнем многочлена , когда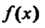Делится на 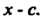Если многочлен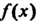Задан формулой (8.3) и

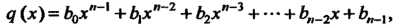
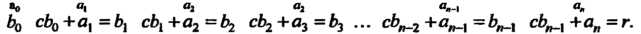
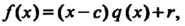
Где

То коэффициенты многочленаОпределяются формулами

(8.5)

А остаток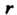- по формуле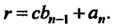

Коэффициенты частного и остаток вычисляются по следующей схеме:

Эту схему, называемую схемой Горнера, используют также для вычисления значений многочлена, Поскольку(см. формулу (8.4)).

Если с - корень многочлена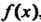, т. е:То многочлен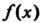Делится

На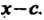Может оказаться, что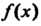Делится и на более высокие степени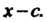

Пусть существует такое натуральное числ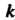о, что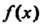Нацело делится на

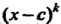, но уже не делится на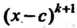. В этом случае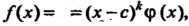

Причем число с не является корнем многочлена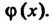Число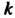Называется кратностью корня с многочлена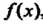, а число с —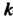-кратным корнем этого многочлена. Если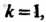То говорят, что число с - простой корень многочлена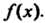

Теорема 8.3. Всякий многочлен, степень которого не меньше единицы, имеет хотя бы один корень (действительный или комплексный).

Эту теорему раньше называли «основной теоремой высшей алгебры».

Следствие. 1. Всякий многочлен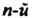Степени единственным образом, с точностью до порядка сомножителей, разлагается в произведение п линейных множителей: если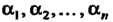— корни многочлена (8.3), то

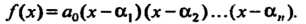(8.6)

Следствие. 2. Всякий многочлен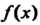Степени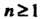ИмеетКорней, считая равные и комплексные.

Следствие. 3. Если многочлены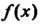И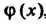, степени которых не

Превышают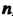, имеют равные значения более чем при п различных значениях переменной. то

Если многочлен

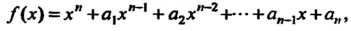(8.7)

Для которого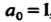, имеет корни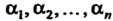, то его коэффициенты выражают

Ся формулами Виета:

(8.8)

Эти формулы Означают следующее: в правой части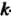-го равенства 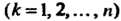Находится сумма всевозможных произведений по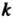Корней, взятая со знаком плюс или минус в зависимости от четности или нечетности.

Последняя из формул (8.-8) свидетельствует о том, что корни многочлена (8.7) являются делителями его свободного члена.

Формулы Виета дают возможность найти многочлен по корням.

Теорема 8.4. Если комплексное число а. является корнем многочлена с действительными коэффициентами, то его корнем будет также и сопряженное число

Следствие. \. Многочлен /(х) в этом случае делится на квадратный трехчлен ф (х) = (х-а) (х-а) = х2 + рх+дс действительными коэффициентами р = -(а + а), 9=оо.

С л е д с т в и е. 2. Комплексные корни всякого многочлена с действительными коэффициентами попарно сопряжены.

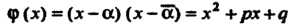
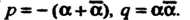
Следствие. 3. Многочлен нечетной степени с действительными коэффициентами имеет хотя бы один действительный корень. Если же действительных корней больше одного, то их будет нечетное число (так как комплексные корни попарно сопряжены).

Следствие. 4. Всякий многочлен с действительными коэффициентами можно представить, причем единственным способом (с точностью до порядка множителей), в виде произведения его старшего коэффициента и нескольких многочленов с действительными коэффициентами, линейных вида х —с, соответствующих его действительным корням, и квадратных вида х2+рх+д, соответствующих парам его сопряженных комплексных корней.

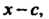
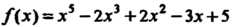
Пример 8.3. Разделить многочлен /(х) = х5 - 2х3 + 1хг - Зх + 5 на х—1. Коэффициенты многочлена: а0 = 1, о, = 0, = -2, а3- 2, а4=- 3, а5= 5.

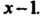
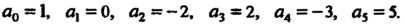
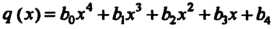
Коэффициенты частного д (х) = Ь0хА + Ь, х3 + ^х2 + Ь}Х + ЬЛ и остаток г находим по схеме Горнера, считая с = Ь

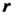
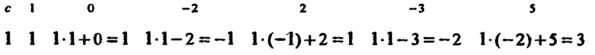
С I  О  -2  2  -3  5

1 1 11 + 0 = 1 1-1 — 2 = —1 1-(-1)+2 = 1 1-1 —3 =—2 1-(-2)+5 = 3 Следовательно, частное д (х) = х4 + х3 - х2 + х - 2, а остаток г = 3.

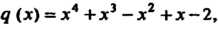
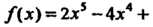
Пример 8.4. Вычислить значение многочлена /(х) = 2х5-4х4 + +5х3—26х2—Ш+9 при х = 3.

По схеме Горнера находим:

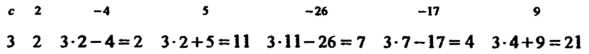
С 2  -4  5  -26  -17  9

3 2 3-2 —4 = 2 3-2 + 5 = 11 3-11-26 = 7 3-7-17 = 4 3-4+9 = 21

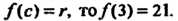
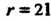
Итак, г = 21; поскольку /(с) = г, то/(3) = 21.

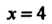
Пример 8.5. Показать, что число х = 4 является корнем многочлена /(х) = Зх4 - 2х3 - 47х2 + ЗОх - 8.

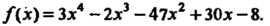
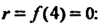
С помощью схемы Горнера находим, что г = /(4) = 0:

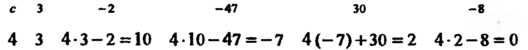
С 3  -2  -47  30  -8

4 3 4-3 - 2=10 4-10 — 47 =—7 4(-7)+30 = 2 4-2 - 8 = 0 Так как г = 0, то /(4) = 0, х = 4 - корень многочлена.

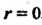
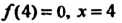
Пример 8.6. Найти многочлен третьей степени, корни которого а, = 1, с&2 =—2, а3 =3.

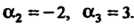
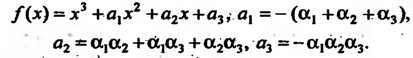
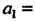
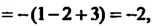
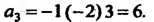
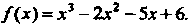
-Воспользуемся формулами Виета. При, п = 3 многочлен (8.7) и формулы (8.8) принимают соответственно вид

/(¦*) = ¦*3 +агх2 +а2х+а3, а, =-(а, +а2 +а3), о2 = а, а2+0]«з+а2а3, о3 =-а, а2аз.

Подставляя в последние три формулы значения корней, получаем а, = = -(1-2 + 3) = -2, а2 = 1-(—2)+1-3+(—2)3 = -5, а3 =-1(-2)3 = 6. Следовав

Тельно, /(х) = хъ - 2х2 - 5л+6.

Пример 8.7. Найти многочлен четвертой степени, имеющий корни а,=-1, 4X2=2, 03=4, а4=5.

При л = 4 многочлен (8.7) и формулы (8.8) запишутся так:

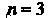
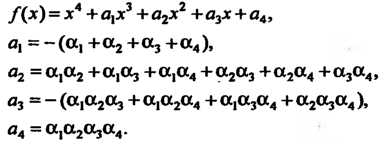
По эти формулам находим о, =-10, а2 = 27, о3=-2, а4 = -40. Итак, Дх) = х4 - 10х3 + 27х2 -2х - 40.

< Предыдущая		Следующая >