08.1. Алгебраические многочлены
Алгебраическим многочленом степени и называется сумма целых неотрицательных степеней переменной х, взятых с некоторыми числовыми коэффициентами, т. е. выражение вида
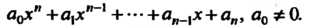
Для сокращенной записи многочленов употребляют обозначения ,
,  И т. п.
И т. п.
Два многочлена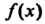 И
И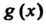 Считают равными и пишут
Считают равными и пишут В том и
В том и
Только в том случае, когда равны их коэффициенты при одинаковых степенях х.
Теорема 8.1. Для любых двух многочленов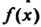 И
И Можно найти такие многочлены
Можно найти такие многочлены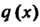 И
И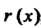 , что
, что
Причем степень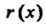 Меньше степени
Меньше степени Или же
Или же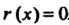 . Многочлены
. Многочлены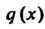
И Определяются однозначно.
Определяются однозначно.
Многочлен Называется частным от деления
Называется частным от деления На
На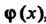 , а
, а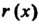 -
-
Остатком от этого деления.
Замечание. Формулу (8.1) можно записать так:
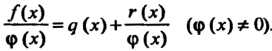
Если остаток от деления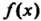 На
На Равен нулю, то многочлен
Равен нулю, то многочлен Называется делителем многочлена
Называется делителем многочлена , в этом случае говорят, что
, в этом случае говорят, что Делится на
Делится на 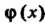 (или нацело делится на
(или нацело делится на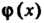 ).
).
Многочлен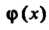 Тогда и только тогда является делителем многочлена
Тогда и только тогда является делителем многочлена
Когда существует многочлен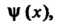 Удовлетворяющий равенству
Удовлетворяющий равенству

Многочлен Называется общим делителем для многочленов
Называется общим делителем для многочленов И
И
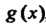 , если он является делителем каждого из этих многочленов.
, если он является делителем каждого из этих многочленов.
Два многочлена называются взаимно простыми, если они не имеют других общих делителей, кроме многочленов нулевой степени (т. е. постоянных).
Наибольшим общим делителем отличных от нуля многочленов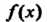 И
И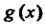 называется общий делитель
называется общий делитель Который делится на любой другой общий де
Который делится на любой другой общий де
Литель этих многочленов. Наибольший общий делитель многочленов И
И
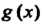 Обозначается так:
Обозначается так: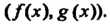
Наибольший общий делитель многочленов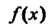 И
И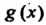 Можно найти с по
Можно найти с по
Мощью алгоритма Евклида. Если
То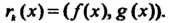
Замечание. Наибольший общий делитель многочленов определен с точностью до постоянного множителя: если — наибольший общий дели
— наибольший общий дели
Тель многочленов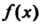 И
И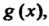 То
То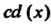 , где
, где - любое 'число, отличное от
- любое 'число, отличное от
Нуля, также является их наибольшим общим делителем.
Пример 8.1. Найти чаЛ-ное И остаток
И остаток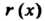 Прн делении много
Прн делении много
Члена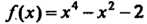 На многочлен
На многочлен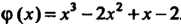 . Выразить
. Выразить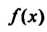
Через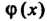 И
И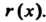
Выполняя деление, находим
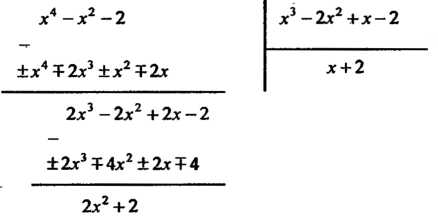
Итак,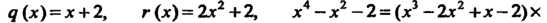
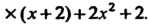

Пример 8.2. Найти общий наибольший делитель двух многочленов 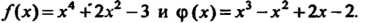
Произведя деление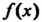 На
На , получим первое из равенств (8.2):
, получим первое из равенств (8.2):
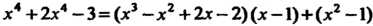 , так как
, так как И
И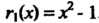
Разделив На
На Найдем второе из указанных равенств:
Найдем второе из указанных равенств:
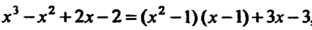 , поскольку
, поскольку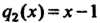 И
И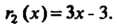
Остаток Нацело делится на остаток
Нацело делится на остаток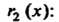
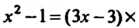
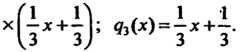
Следовательно,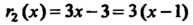 Является общим наибольшим делите
Является общим наибольшим делите
Лем данных многочленов. В соответствии с замечанием общим наибольшим делителем будет также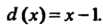
| < Предыдущая | Следующая > |
|---|