07.6. Действия над комплексными числами, заданными в тригонометрической форме
Произведение двух комплексных чисел

Где Находится по формуле
Находится по формуле
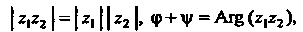
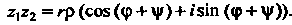
(7.30)
(7.31)
Из этой формулы следует, что
Т. е. модуль произведения равен произведению модулей множителей, а сумма аргументов множителей является аргументом их произведения.
Если , то
, то
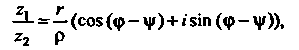
(7.32)
Откуда
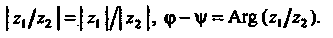
Эти формулы означают, что модуль частного равен модулю делимого, деленному на модуль делителя, а разность аргументов делимого и делителя является аргументом частного двух комплексных чисел.
Если То
То
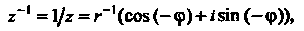 (7.33)
(7.33)
Откуда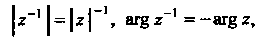
Т. е. модуль комплексного числа , обратного числу
, обратного числу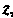 , равен обратной величине модуля числа
, равен обратной величине модуля числа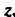 А его главное значение аргумента отличается от главного значения аргумента
А его главное значение аргумента отличается от главного значения аргумента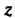 Лишь знаком.
Лишь знаком.
Если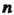 — натуральное число и
— натуральное число и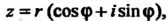 То
То
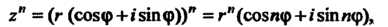 (7.34)
(7.34)
Откуда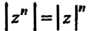
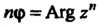
Формула (7.34) называется формулой Муавра. При Она принимает вид
Она принимает вид
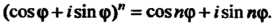
Корнем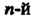 Степени из комплексного числа
Степени из комплексного числа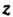 Называется такое комплексное число
Называется такое комплексное число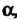 Что
Что
Извлечение корня Степени из комплексного числа
Степени из комплексного числа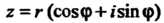 Все
Все
Гда возможно и дает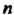 Различных значений:
Различных значений:
(7.35)
Где

Из формул видно, что все п значений корня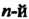 Степени из комплексного числа
Степени из комплексного числа
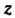 Расположены на окружности радиуса
Расположены на окружности радиуса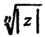 С центром в точке нуль и делят эту
С центром в точке нуль и делят эту
Окружность на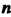 Равных частей.
Равных частей.
Отметим, что корень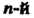 Степени из действительного числа также имеет п различных значений. Среди этих значений действительных будет два, одно или ни одного в зависимости от знака
Степени из действительного числа также имеет п различных значений. Среди этих значений действительных будет два, одно или ни одного в зависимости от знака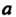 И четности
И четности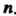 Корень
Корень Степени из нуля имеет
Степени из нуля имеет
Только одно значение, равное нулю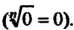
Корни и-й степени из единицы определяются формулой
 (7.37)
(7.37)

Пример 7.7. Найти значения квадратного корня из числа Представим сначала это число в тригонометрической форме:
Представим сначала это число в тригонометрической форме:  В соответствии с формулой (7.36) имеем
В соответствии с формулой (7.36) имеем
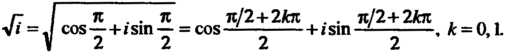

Следовательно, 
Пример 7.8. Найти все значения корня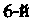 Степени из числа
Степени из числа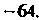 Представим данное число в тригонометрической форме:
Представим данное число в тригонометрической форме: 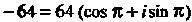 . Формула (7.36) принимает вид
. Формула (7.36) принимает вид
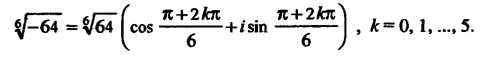
Замечая, что И придавая
И придавая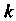 Указанные значения, находим шесть ис
Указанные значения, находим шесть ис
Комых значений:

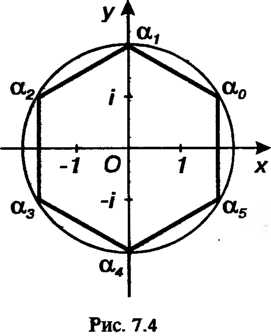
Эти значения изображаются вершинами правильного шестиугольника, вписанного в окружность радиуса (рис. 7.4.).
(рис. 7.4.).
Пример 7.9. Решить уравнение
Так как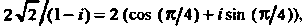 То
То

Применяя формулу (7.36), получаем 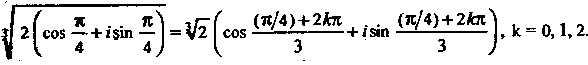 Полагая в этой формуле
Полагая в этой формуле , находим
, находим
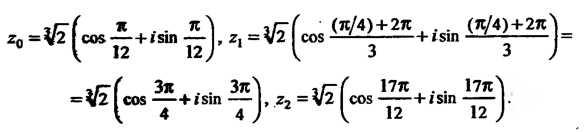
| < Предыдущая | Следующая > |
|---|