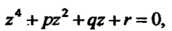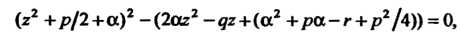08.5. Уравнения четвертой степени
Алгебраическое уравнение четвертой степени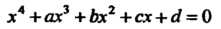 
с помощью подстановки
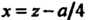Можно привести к уравнению
В котором коэффициент при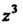
Равен нулю.
Это уравнение можно записать так:
Где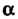
- вспомогательный параметр. Значение параметра выберем так, чтобы вычитаемый многочлен был полным квадратом. В этом случае многочлен имеет два равных корня, так как его дискриминант равен нулю, т. е.
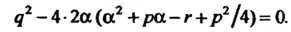(8.23)
Уравнение (8.22) принимает вид
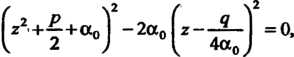
(8.24)
Где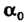
- отличный от нуля корень уравнения (8.23).
Уравнение (8.24) распадается на два квадратных уравнения:
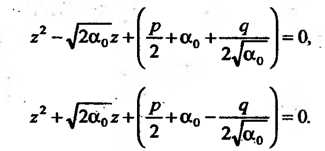
Корни этих уравнений будут корнями уравнения (8.21).
Пример 8.12. Решить уравнение 24 - 5г2 + 4=0.
Это уравнение вида (8.21), для которого р = - 5, 9 = 0, г = 4. Уравнение (8.23) в данном случае сводится к квадратному уравнению относительно параметра а:а2-5а—4+25/4=0, или а2 - 5а+9/4 = 0, которое имеет корни а, =9/2, а2 = 1/2. При а0 = 1/2 уравнения (8.25) запишутся так: г2 - г - 2=0, г2+2-2 = 0. Первое из них имеет, корни *,=—!, г2=2, а второе - г, =1, г2 = -2. Эти числа являются и корнями исходного уравнения.
Пример 8.13. Решить уравнение х4 +4х3 + 7х2 - 4х—8 = 0. Разложим на множители многочлен в левой. части уравнения:
Х4 +4*3 +7х2 - 4х - 8 = (х4 - х2)+(4*3 - 4х)+(8х2 - 8) = х2(х2 - 1)+4х (х2 -1)+
+ 8 (х2 -1) = (х2 -1) (х2 + 4х + 8).
Следовательно, уравнение примет вид (х2 -1)(х2 +4х+8) = 0, откуда х2 —1 = 0, хг+4х + 8 = 0; Х\ = — 1, х2 = 1, х3 = — 2 + И, х4 = —2 — 2/.
| < Предыдущая | Следующая > |
|---|
