07.4. Действия над комплексными числами
Из определения комплексного числа (как упорядоченной пары действительных чисел) и определения арифметических действий над упорядоченными парами (см. формулы (7.3), (7.4), (7.6), (7.7)) следует, что
(7.15)
(7-16)
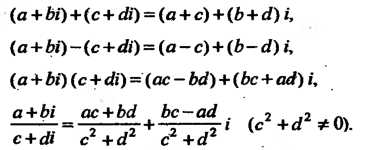 (7.17)
(7.17)
Формула (7.14) определяет правило сложения двух комплексных чисел: чтобы сложить два комплексных числа, необходимо сложить отдельно их действительные и мнимые части. Формула (7.15) означает, что при вычитании одного комплексного числа из другого необходимо вычесть отдельно их действительные и мнимые части.
Отметим, что сумма и произведение двух комплексно-сопряженныхчисел 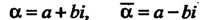 Являются действительными числами:
Являются действительными числами: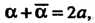
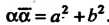
Арифметические действия над комплексными числами подчиняются тем же законам, что и действия над действительными числами. Если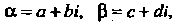
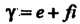 — любые комплексные числа, то верны следующие равенства:
— любые комплексные числа, то верны следующие равенства:
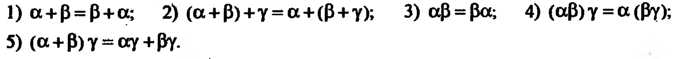
Полагая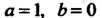 В формуле (7.17), получаем
В формуле (7.17), получаем
 (7.18)
(7.18)
Формулой (7.18) определяется число , обратное комплексному числу
, обратное комплексному числу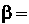

Натуральные степени мнимой единицы < принимают лишь четыре значения: 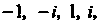 Определяемые формулами
Определяемые формулами
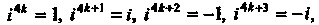 (7.19)
(7.19)
Где
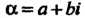
При возведении комплексного числа а = а+ Ы в степень и (я - натуральное число) пользуются формулой бинома Ньютона:

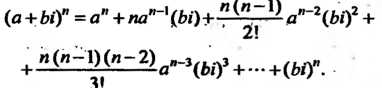
(а+Ы)" = а" + па"-'(Ы)+П дв-2(Ы)2 +
+ —V. а”~\ьО3 + - +(&')"• (7-20)
В правой части этого равенства заменяют степени мнимой единицы по формулам (7.19) и приводят подобные члены, в результате получают Некоторое комплексное число с+<Л.
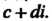
Квадратным корнем из комплексного числа называют комплексное число, квадрат которого равен данному комплексному числу:
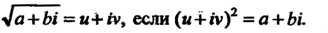
Т! а+Ы = и+ы, если (и+п)2 =а+Ьй (7-21)
Числа и и V определяются из равенств
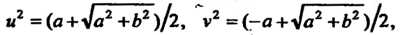
И2 = (о + у1а2+Ь2)/г, V =(-а + 4а2+Ь2 )Д, (7.22)
% *
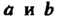

Причем и и V будут действительными, так как при любых а и Ъ выражения <з + >/<а2 +Ь2 и - а+у! а2 +Ь2 являются положительными. Знаки и и V выбирают так, чтобы выполнялось равенство 2т> = Ь. Извлечение квадратного корня из комплексного числа а+Ы всегда возможно и дает два значения и, + «V,, щ + г»г, различающихся лишь знаком.



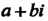
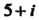
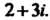
Пример 7.1. Даны два комплексных числа 5+/ и 2+3/. Найти их сумму, разность, произведение и частное.
В соответствии с формулами (7.14) — (7.17) получаем

(5+/)+(2+3/)у (5+2)+(1 + 3)/=7+4/,
(5+/) - (2+3») = (5 - 2)+(1 - 3) / = 3 - 2/,
(5+/)(2+3/) = 10+15/+2/+3/2 = 7+17/,
5+/ _ (5+/)(2-3/) __ 10—15/+2/-3/2 = 13-13/ _ .
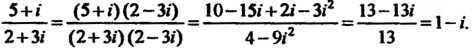
2+3/ (2+3/)(2-3/) 4 - 9/2 13 *'
Пример 7.2. Возвести в указанные степени данные комплексные числа:
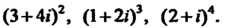
(3+4/)2, (1 + 2/)3, (2+04-
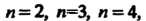
Применяя формулы (7.19) и (7.20) при л = 2, и=3, л = 4, получаем

¦ (3+4/)2 =32 +2-12/+(4/)2 = 9+24/+16/2 =-7+24/,
(1+2/)3 =1+6/+12/2 +8/3 =1+6/—12—8*=—11 — 2/,
(2+/)4 =24 +4-23»'+6-4/2 +4-2/3 +/4 =16+32*—24—8/+1 =-7+24/.
Пример 7.3. Извлечь корень квадратный из числа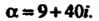 Обозначим
Обозначим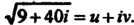 Поскольку в данном случае
Поскольку в данном случае То
То
Формулы (7.22) примут вид

Так как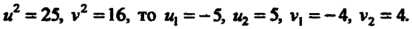 Получено два значения
Получено два значения
Кория: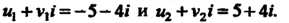
Пример 7.4. Найти значение выражения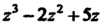 При
При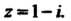
Поскольку
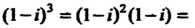
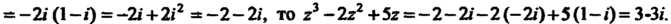
Пример 7.5. Показать, что комплексное число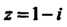 Является корнем
Является корнем
Уравнения
Так как
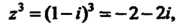 То
То
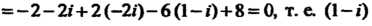 - корень уравнения.
- корень уравнения.
| < Предыдущая | Следующая > |
|---|