07.3. Геометрическое изображение комплексных чисел

 

На плоскости выберем систему прямоугольных декартовых координат (рис. 7.1). Комплексному числу (а, Ь)= а + Ы сопоставим точку Л/(с, Ь) этой

Плоскости с координатами (а, Ь). Если Ь = 0, то получим действительное число (а, 0) = а, которое изображается точкой А (о, 0) на оси Ох. Вследствие этого ось Ох называют действительной осью (точками оси абсцисс изображаются действительные числа). Если а = 0, то получаем чисто мнимое число Ы, которое изображается точкой В(0,Ь), лежащей на оси Оу. По этой причине ось ординат на-р _ .  зывают мнимой осью (точками этой оси изобража

Ются чисто мнимые числа). Отметим, что мнимая единица« изображается точкой (0,1), расположенной на положительной полуоси ординат и отстоящей от начала координат на расстояние, равное единице. Число (—/) изображается на оси ординат точкой (0,-1), симметричной точке (0,1). Любое комплексное число а = (а, Ь), где а Ф 0, Ьф 0, изображается точкой, не лежащей на осях координат. Обратно, любой точке М (а, Ъ) плоскости соответствует комплексное число (а, Ь) = а + Ы. Таким образом, между множеством ком-

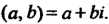
5 Зак. 1

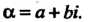
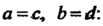
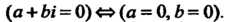
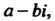
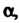
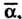
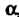
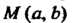
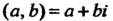
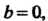
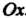
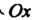
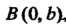
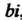
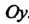
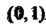
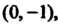
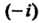
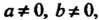
129

 

Плексных чисел и множеством точек плоскости установлено взаимно однозначное соответствие. Плоскость, точки которой отождествлены с комплексными числами, называют комплексной плоскостью.

Рассматривают также комплексную переменную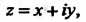Где-

Действительные переменные,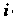- мнимая единица. Значения этой переменной-комплексные числа, изображаемые точками комплексной плоскости.. Вследствие этого комплексную плоскость называют также плоскостью, комплексной переменной.

< Предыдущая		Следующая >