07.2. Понятие комплексного числа. Алгебраическая форма комплексного числа
Комплексным числом называют упорядоченную пару Действительных
Действительных
Чисел акЬ. Рассмотрим упорядоченную пару
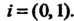 (7.10)
(7.10)
Применяя формулу (7.4), получаем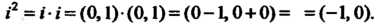 Поскольку
Поскольку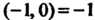 (см. формулу (7.9)), то
(см. формулу (7.9)), то
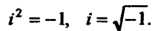 (7.11)
(7.11)
Упорядоченную пару (7.10), удовлетворяющую соотношению (7.11), называют мнимой единицей. С помощью мнимой единицы можно выразить любое комплексное число , т. е. упорядоченную пару действительных чисел. В самом деле, так как
, т. е. упорядоченную пару действительных чисел. В самом деле, так как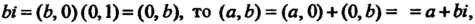 Т. е.
Т. е.
 (7.12)
(7.12)
Поскольку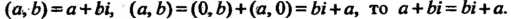 Значит,
Значит,
В правой части формулы (7.12) можно менять местами слагаемые. Выражение 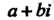 Называют алгебраической формой комплексного числа. Число
Называют алгебраической формой комплексного числа. Число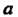 Называют действительной частью,' число
Называют действительной частью,' число — мнимой частью комплексного числа
— мнимой частью комплексного числа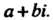 Обозначая комплексное число
Обозначая комплексное число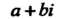 Одной буквой
Одной буквой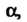 Записывают
Записывают
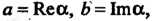 Где Re - начальные буквУ латинского слова realis
Где Re - начальные буквУ латинского слова realis
(действительный), Im - начальные буквы латинского слова imaginarius (мнимый).
Кроме этих обозначений, употребляют и другие, например; а = Я (а), Ь — / (а), где а = а + Ы.
Отметим частные случаи формулы (7.12). Если Ь = О, то (о, 0) = в— действительное число; если а = 0, то
(О, Ь) = Ы. (7,13)
Число Ы называют чисто мнимым или Просто мнимым.
Два комплексных числа а + Ы, с + называют равными, когда а = с, Ь = 4:
(а + Ы = с + Ш) <=> (а = с, Ь = с1).
Комплексное число равно нулю, когда равны нулю его действительная и мнимая части:
(о + Ы = 0)<=>(а = 0,Ь = 0).
Если дано комплексное число а = а + Ы, то число а - Ы, отличающееся от а только знаком при мнимой части, называют числом, сопряженным числу ос, и обозначают а. Числом, сопряженным а, будет, очевидно, число а, поэтому говорят о паре сопряженных чисел. Действительные числа, и только они, сопряжет сами себе.
Обозначение (для мнимой единицы (/= ^-1) ввел Эйлер в 1777 г.
| < Предыдущая | Следующая > |
|---|