07.1. Упорядоченные пары действительных чисел и операции над ними

 

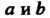ПаруДействительных чиселНазывают упорядоченной, если указа

Но, какое из них считается первым, какое - вторым. Примеры упорядоченных пар: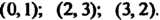Отметим, что последние две пары различны, хотя и об

Разованы одними и теми же числами.

Каждую упорядоченную пару чисел обозначим одной буквой, введем понятие равенства двух пар, определим действия над ними. Рассмотрим две упорядоченные пары

Эти лары называют равными, если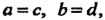Т. е.

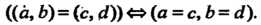
Суммой двух пар (7.1) называют упорядоченную пару 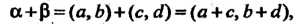 а их произведением — упорядоченную пару

(7.1)

(7.2)

(7.3)

(7.4)

 

Из соотношения (7.3) видно, что пара

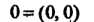(7.5)

Обладает тем свойством, что сложение ее с любой другой упорядоченной парой не меняет исходной парЫ: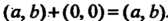. Пара (715) играет роль нуля при

Сложении упорядоченных пар; назовем ее нуль-парой.

Разностью. двух упорядоченных пар (7.1) называют такую упорядоченную пару

Вычитание упорядоченных пар (7.1) определяется следующим образом:

(7.6)

Частным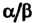, где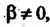Двух упорядоченных пар (7.1) называют такую упо

Рядоченную пару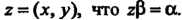

ЕслиТо частное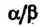Двух упорядоченных-пар (7.1)

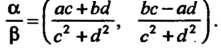(7.7)

Из этой формулы следует, что если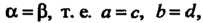То

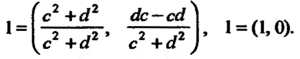
Значит,-роль единицы при делении двух упорядоченных пар выполняет упорядоченная, пара

(7.8)

Рассмотрим упорядоченные пары

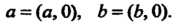(7.9)

Арифметические действия над упорядоченными парами вида (7.9) производятся так, как и над действительными числами. Действительные числа отождествляются с парами вида (7.9).

< Предыдущая		Следующая >