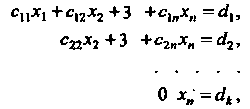06.5. Метод Гаусса
Пусть дана система (6.1) т линейных алгебраических уравнений с п неизвестными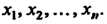
Метод последовательного исключения неизвестных, или метод Гаусса, применяемый для решения системы (6.1), состоит в следующем.
Предполагая, что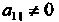
(это всегда можно сделать сменой нумерации
Уравнений), умножая первое уравнение системы (6.1) на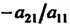
И прибав
Ляя ко второму, получаем уравнение, в котором коэффициент при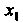
Обращается в нуль. Умножая первое уравнение на
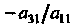И прибавляя к третьему, получаем уравнение, также не содержащее члена с
. Аналогичным путем преобразуем все остальные уравнения, в результате чего придем к системе, эквивалентной исходной системе уравнений:
Отличен от нуля, ему соответ-
Где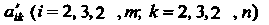
— некоторые новые коэффициенты.
Полагая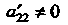
И оставляя неизменными первые два уравнения системы
(6.17), преобразуем ее так, чтобы в каждом из остальных уравнений коэффициент при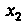
Обратился в нуль. Продолжая этот процесс, систему (6.17) можно привести к одной из следующих систем:
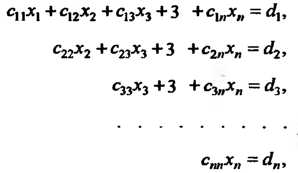(6.18)
Где
— некоторые коэффициенты,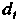
— свободные члены;
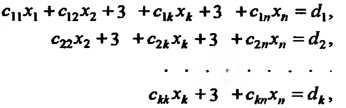(6.19)
Где
Система (6.18) имеет единственное решение, значение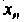
Находится из последнего уравнения,
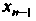- Из предпоследнего,
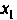- из первого.
Система (6.19) имеет бесконечное множество решений. Из последнего уравнения можно выразить одно из. неизвестных (например,
) через остальные
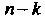неизвестных
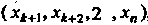, входящих в это уравнение. Из предпоследнего
Уравнения можно выразить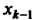
Через. эти неизвестные и т. д. В полученных формулах, выражающих
Нерез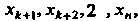
Последние неизвестные могут принимать любые значения.
Система (6.20) несовместна, так как никакие значения неизвестных не могут удовлетворять ее последнему уравнению.
Итак, метод последовательного исключения неизвестных применим к любой системе линейных уравнений. Решая систему этим методом, преобразования совершаются не над уравнениями, а над матрицами, составленными из коэффициентов при неизвестных и свободных членах.
Пример 6.S. Решить систему уравнений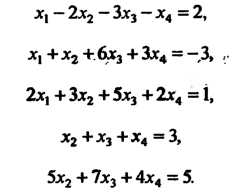 
Составляем матрицу и преобразуем ее:
Последней матрице соответствует совместная система четырех уравнений с четырьмя неизвестными:
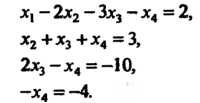
Решая эту систему, находим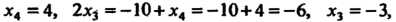
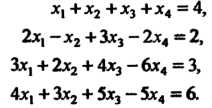
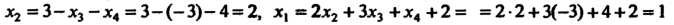
Следовательно, исходная система имеет решение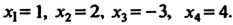
Пример 6.6. Решить систему уравнений
Записывая соответствующую матрицу и совершая преобразования, получаем
Третья матрица получена из предыдущей переменой местами последних трех строк. Последней матрице соответствует система уравнений
Эта система несовместна, так как никакие значения неизвестных не могут удовлетворить ее третьему уравнению.
Следовательно, исходная система также несовместна.
Пример 6.7. Решить систему уравнений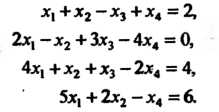 
Таким образом, данная система сводится к системе двух уравнений относительно четырех неизвестных:
Общее решение которой определяется формулами
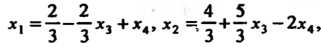
Где х3, хл могут принимать любые действительные значения.
Пример 6.8. Решить систему уравнений
Составляем матрицу и преобразуем ее:
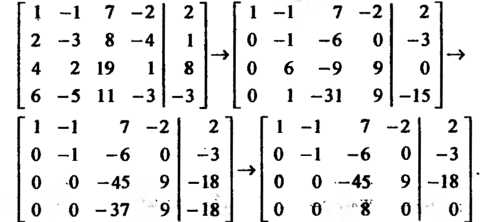
Последняя матрица получена в результате сложения третьей, умноженной на 
, и четвертой строк. Этой матрице соответствует система уравнений
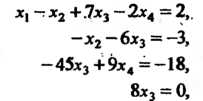F
Имеющая решение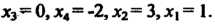
| < Предыдущая | Следующая > |
|---|
