06.3. Невырожденные линейные системы

 

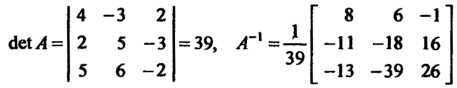
По формуле (6.16) получаем решение системы

Рассмотрим линейную систему (6.1), ее основную матрицу А и расширенную А, определяемую формулой (6.5).

Теорема 6.2. (Кронекера — Капелли). Для совместности системы (6.1) необходимо и достаточно, чтобы ранг ее матрицы был равен рангу расширенной матрицы.

Теорема 6.3. Если ранг матрицы совместной системы равен числу неизвестных, то система имеет единственное решение.

Теорема 6.4. Если ранг матрицы совместной системы меньше числа неизвестных, то множество ее решений является бесконечным.

Базисным минором матрицы называется отличный от нуля ее минор, порядок которого равен рангу этой матрицы. Базисными неизвестными совместной системы, ранг матрицы которой равен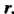, назовемНеизвестных, коэффициенты при которых образуют базисный минор. Остальные неизвестные назовем свободными.

Из теорем 6.2 - 6.4 следует, что решение системы линейных уравнений можно производить следующим образом.

1.  Находят ранг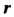Матрицы А системы и ранг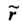Расширенной матрицы Бели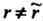, то система несовместна.

2.  Если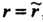, то выделяют базисный минор и базисные неизвестные. Исходную систему уравнений заменяют эквивалентной ей системой, состоящей из тех 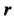уравнений, в которые вошли элементы базисного минора.

Отметим, что в случае, когда число базисных неизвестных равно числу неизвестных системы, система имеет единственное решение, которое можно найти по формулам Крамера Если число базисных неизвестных меньше числа всех неизвестных, то из соответствующей системы находят выражения базисных неизвестных через свободные, используя, например, формулы Крамера Придавая свободным неизвестным произвольные значения, получают бесконечное множество решений исходной системы.

Пример 6.4. Решить систему уравнений  Поскольку

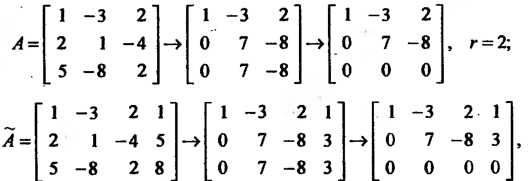
То система совместна. В матрице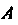Минор

Ствует система уравненийВ которой

- базисные неизвестные,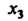- свободная неизвестная. Решая эту систему по формулам Крамера, находим

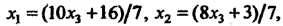
Где х3 может принимать любые действительные значения.

< Предыдущая		Следующая >