06.2. Матричная запись линейной. системы
Линейную систему (6.1) можно записать в матричном виде. Матрица
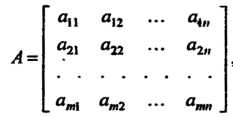
(6.4)
Составленная из коэффициентов линейных уравнений системы (6.1), называется основной матрицей системы (или матрицей системы). Матрица
(6.5)
Полученная из основной присоединением столбца свободных членов, называется расширенной матрицей системы (6.1).
Рассмотрим столбцовые матрицы, составленные из неизвестных и свободных членов:
Поскольку матрица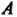
Согласована с матрицей
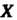(число столбцов матрицы
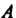Равно числу строк матрицы
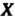), то можно найти произведение
Элементами этой столбцовой матрицы являются левые части уравнений системы
(6.1), поэтому на основании определения равенства матриц
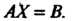(6.7)
Таким образом, система линейных уравнений (6.1) записана в виде одного матричного уравнения (6.7), где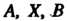
Определяются формулами (6.4) и (6.6); эта запись системы называется матричной.
Каждой линейной системе (6.1) соответствует единственная пара матриц
И обратно: каждой паре матриц - единственная линейная система. Система (6.1) может быть записана и в таком виде
(6.9)
Называется вектор-решением этой системы. Матрица (6.9) удовлетворяет уравнению (6.7). Пример 6.1. Представить в матричной форме линейную систему уравнений
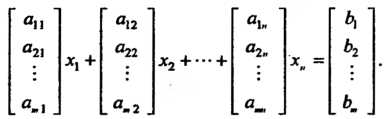
Если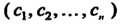
— решение системы (6.1), то матрица
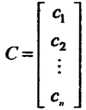
В данном случае формулы (6.4) и (6.6) запишутся так:
Поэтому уравнение (6.7) принимает ввд
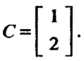
Эта система имеет вектор-решение
Замечание. В соответствии с формулой (6.8) данная система представима в виде
| < Предыдущая | Следующая > |
|---|
