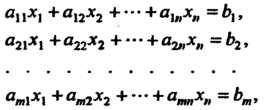06.1. Линейные системы. Основные определения
Системой уравнений называют множество уравнений с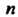
Неизвестными 
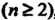, для которых требуется найти значения неизвестных, удовлетворяющих одновременно всем уравнениям системы.
Системой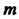
Линейных уравнений с ц неизвестными
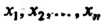Или линейной
Системой, называется система вида
Где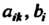
— числа Числа
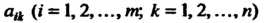Называются коэффи
Циентами,
- свободными членами. Коэффициенты обозначены
Буквой а с двумя индексами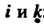
: первый
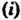Указывает номер уравнения, второй 
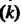- номер неизвестной, к которой относится данный коэффициент. Число уравнений т может быть больше, равно или меньше числа неизвестных
.
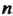Линейная система называется неоднородной, если среди свободных членов имеются отличные от нуля. Если все свободные члены равны нулю, то линейная система называется однородной. Однородная линейная система имеет вид
Решением линейной системы (6.1) называется упорядоченная совокупность п чисел
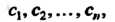(6-3)
Подстановка которых вместо
Соответственно
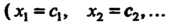
Обращает в тождество каждое из уравнений этой системы.
Система, имеющая хотя бы одно решение, называется совместной, а система, не имеющая ни одного решения, - несовместной. Отметим, что однородная система всегда совместна, так как она имеет нулевое решение:
Совместная система, имеющая единственное решение, называется определенной. Совместная система называется неопределенной, если она имеет более одного решения.
Две системы называются эквивалентными или равносильными, если любое решение одной из них является также решением другой и обратно, т. е. если они имеют одно и то же множество решений. Любые две несовместные системы считаются эквивалентными.
Элементарными преобразованиями линейной системы называются следующие преобразования: 1) умножение уравнения системы на число, отличное от нуля;
2) прибавление к одному уравнению другог о уравнения, умноженного на любое число; 3) перестановка местами двух уравнений системы.
При элементарных преобразованиях линейной системы получают систему, равносильную данной.
Выражение «решить линейную систему» означает выяснить, совместна она или несовместна; в случае совместности - найти все ее решения.
| < Предыдущая | Следующая > |
|---|
