05.6. Ранг матрицы
Рассмотрим матрицу размером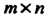
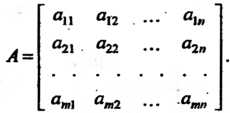
Выберем в ней произвольно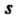
Различных строк и
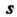Различных столбцов, причем
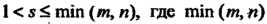- меньшее из чисел
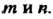Элементы, стоящие на
Пересечении выбранных строк и столбцов, образуют матрицу порядка s. Определитель этой матрицы называется минором порядка s матрицы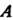
. Например, если дана матрица
То, взяв первую и третью строку, третий и пятый столбец, получим матрицу второго порядка и ее определитель
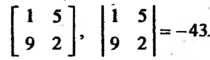
Этот определитель является минором второго порядка для исходной матрицы. Аналогично можно получить другие миноры второго порядка, а также миноры третьего порядка Некоторые из миноров могут оказаться равными нулю.
Рангом матрицы называется наибольший из порядков ее миноров, отличных от нуля. Ранг матрицы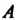
Обозначают одним из символов:
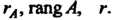Если все
Миноры матрицы равны нулю, то ранг ее считается равным нулю.
Из определения ранга матрицы получаем следующие утверждения.
1. Ранг матрицы выражается целым числом, заключенным между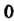
И меньшим из чисел
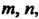Т. е.
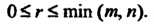
.... Ранг матрицы равен нулю тогда и только тогда, когда матрица нулевая.
3. Для квадратной матрицы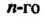
Порядка
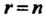Тогда и только тогда, когда матрица невырожденная.
При нахождении ранга матрицы можно пользоваться свойствами миноров. Если все миноры порядка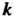
Данной матрицы равны нулю, то все миноры более высокого порядка также равны нулю. Таким образом, если среди миноров порядка
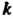Данной матрицы есть отличные от нуля, а все миноры порядка
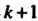Равны нулю или не существуют, то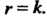
Отметим некоторые очевидные свойства ранга матрицы..
1. Ранг матрицы, полученной из данной транспонированием^ равеи рангу исходной Матрицы.
2. Ранг матрицы не изменится, если вычеркнуть или приписать нулевую строку (т. е. строку, все элементы которой равны нулю) или нулевой столбец.
При элементарных преобразованиях ранг матрицы не меняется.
Помощью элементарных преобразований матрицу можно привести к квазитреугольной форме. Ранг квазтреугольной матрицы (5.1) равен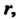
Поскольку ее минор с главной диагональю
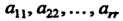Равен произведению
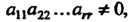А все миноры
Более высокого порядка равны нулю (как содержащие нулевые строки).
Пример 5.15. Найти ранг матрицы
1
Среди. миноров второго порядка этой матрицы имеется один, отличный отнуля:
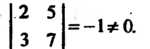
Все миноры третьего порядка равны нулю. Следовательно, ранг данной матрицы равен двум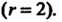
Пример 5.16. Найти ранг матрицы
Применяя элементарные преобразования, приводим данную матрицу к квазитреугольной форме:
(Вторая матрица получена из первой путем поочередного умножения первой строки на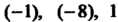
И прибавления ко второй, третьей и четвертой строкам;
Третья матрица получена из второй путем прибавления второй строки к третьей.)
Ранг последней матрицы равен Трем, так как имеется отличный от нуля минор третьего порядка этой матрицы ,
'•51 • "* ' '• ‘
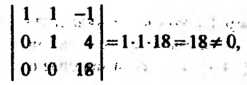
А определитель самой матрицы (определитель четвертого порядка) равен нулю (как содержащий нулевую строку). Следовательно, ранг исходной матрицы равен трем'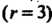
. '¦1 ' '
| < Предыдущая | Следующая > |
|---|
