05.4. Определители и их свойства
Определителем квадратной матрицы второго порядка
Называется число, равное
И обозначаемое символом
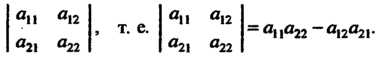
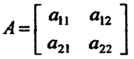
(5.8)
Порядка. Каждый элемент определителя обозначен буквой
С двумя индексами; первый (1) обозначает номер строки, второй (2) - номер столбца, на пересечении которых находится соответствующий элемент (например, элемент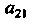
Принадлежит второй строке И первому столбцу определителя).
Определитель матрицы называют также детерминантом. Для определителя матрицы употребляются следующие обозначения:
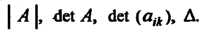
Определителем квадратной матрицы третьего порядка 
Называют число
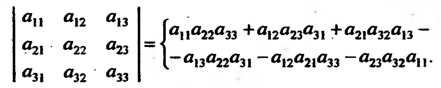
(5.9)
Заметим, что каждое слагаемое алгебраической суммы в правой части этой формулы представляет собой произведение элементов определителя, взятых по одному и только по одному из каждой строки и каждого столбца. Этому произведению приписывается соответствующий знак. Чтобы запомнить, какие произведения следует брать со знаком плюс, какие со знаком минус, полезно правило, схематически изображенное на рис. 5.1.
Минором какого-либо элемента определителя называется определитель, полученный из данного вычеркиванием той строки и того столбца, которым принадлежит данный элемент. Минор элемента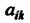
Обозначим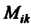
Алгебраическим дополнением элемента
Определителя называется его минор, взятый со знаком
. Алгебраическое дополнение элемента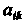
Будем обозначать через
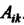. В соответствии с определением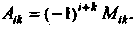
Определители матриц второго порядка и третьего порядка короче называют определителями второго и третьего порядка.
Свойства определителей:
1) определитель не изменится при замене всех его строк соответствующими столбцами;
2) при перестановке двух соседних строк (столбцов) определитель меняет лишь знак;
3) определитель с двумя одинаковыми строками (столбцами) равен нулю;
4) множитель, общий для элементов некоторой строки (столбца), можно вынести за знак определителя;
5) определитель равен нулю, если все элементы некоторой строки (столбца) равны нулю;
6) определитель не изменится, если к элементам некоторой строки (столбца) прибавить соответствующие элементы другой строки (столбца), предварительно умножив их на один и тот же множитель;
7) определитель равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения.
Например,
, т. е.
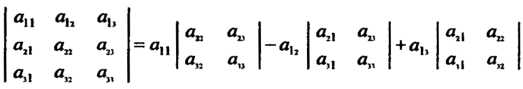
(5.10)
Эта формула выражает разложение определителя третьего порядка по элементам первой строки.
По аналогии с формулой (5.10) вводятся определители четвертого порядка:
(5.11)
Или
Где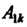
- алгебраическое дополнение элемента
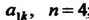; определители пятого
Порядка и т. д.
Теорема 5.1 (теорема замещения). Суммы произведений произвольных чисел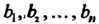
Соответственно на алгебраические дополнения элементов
Некоторого столбца (троки) матрицы порядка п равны определителю матрицы, которая получается из данной заменой элементов этого столбца (строки) числами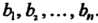
Т е о р е м а 5.2 (теорема аннулирования). Сумма произведений элементов одного из столбцов (трок) матрицы на соответствующие алгебраические дополнения элементов другого столбца (троки)равна нулю.
Теорема 5.3. Определитель произведения двух квадратных матриц
одного порядка равен произведению определителей перемножаемых матриц:
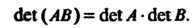
Название «детерминант» предложил Гаусс. Современное изложение теории определителей дал Коши. Обозначение определителя в виде квадратной таблицы чисел с двумя вертикальными чертами ввел Кэли в 1841 г. ,
Пример 5.7. Вычислить определитель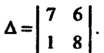
В соответствии с формулой (5.8) получаем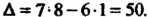
Пример 5.8. Вычислить определитель
Умножая первую строку на —1 и прибавляя ко второй, находим
Пример 5.9. Вычислить определитель третьего порядка
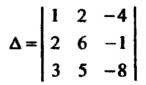
Тремя способами: !)по определению; 2) по формуле (5.10); 3) преобразованием его с помощью свойств.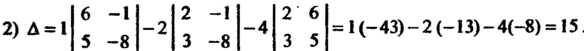 
3) Умножая первую строку на (-2) и прибавляя ко второй, затем умножая
Первую строку на (- 3) и прибавляя к третьей, получаем
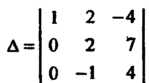
Разлагая этот определитель по элементам первого столбца, находим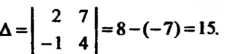 
Применяя формулу (5 Л1), получаем
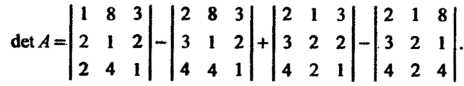
Вычисляя определители третьего порядка, находим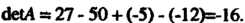
3 а м е ч аи и е. Этот определитель можно вычислить путем его преобразований на основании свойств:
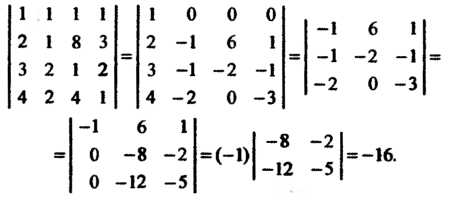
| < Предыдущая | Следующая > |
|---|
