05.3. Произведение матриц. Многочлены от матриц
Произведение определяется для квадратных матриц одного и того же порядка, а также для прямоугольных матриц, у которых число столбцов матрицы множимого равно числу строк матрицы множителя.
Произведением матрицы На матрицу
На матрицу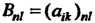 Называется та
Называется та
Кая матрица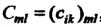 , для которой
, для которой
(5.6)
Т. е. элемент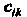 Матрицы равен - сумме произведений элементов ?-й строки матрицы
Матрицы равен - сумме произведений элементов ?-й строки матрицы На соответствующие элементы
На соответствующие элементы Столбца матрицы
Столбца матрицы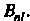 Матрица
Матрица 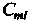 Имеет
Имеет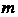 Строк (как и матрица
Строк (как и матрица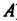 ) И
) И Столбцов (как и матрица
Столбцов (как и матрица ). Произведение матрицы
). Произведение матрицы На матрицу
На матрицу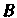 Обозначается
Обозначается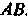
Замечание. Из того, что матрицу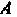 Можно умножить на
Можно умножить на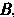 , не следует, что матрицу В можно умножать на
, не следует, что матрицу В можно умножать на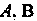 Общем случае
Общем случае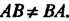 Бели
Бели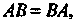 То
То
Матрицы А и В называются перестановочными или коммутативными.
При умножении матриц единичная матрица Е играет роль единицы, а нулевая матрица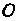 — роль нуля, так как
— роль нуля, так как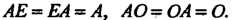
Умножение матриц обладает следующими свойствами. Если имеют смысл соответствующие действия, то выполняются равенства:
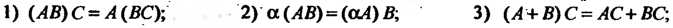
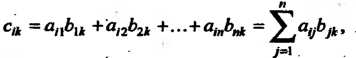
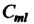
Где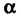 - любое действительное число.
- любое действительное число.

Отметим, что , где штрихом обозначена матрица, транспо
, где штрихом обозначена матрица, транспо
Нированная данной.
Целой положительной степенью Квадратной матрицы
Квадратной матрицы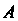 Называется
Называется
ПроизкДение к матриц, каждая из которых равна , т. е.
, т. е.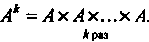 . Мат
. Мат
Рица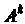 Имеет тот же порядок, что и матрица
Имеет тот же порядок, что и матрица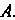 . Нулевой степенью квадратной матрицы
. Нулевой степенью квадратной матрицы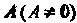 Называется единичная матрица того же порядка, что и
Называется единичная матрица того же порядка, что и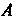 , т. е.
, т. е.
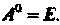 Первой степенью
Первой степенью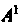 Матрицы
Матрицы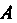 Называется сама матрица
Называется сама матрица , т. е.
, т. е.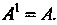 Многочленом (или полиномом) степени
Многочленом (или полиномом) степени (
( -> целое неотрицательное число) от квадратной матрицы
-> целое неотрицательное число) от квадратной матрицы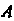 Называется выражение вида
Называется выражение вида
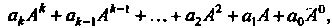
Где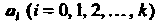 - любые числа, причем
- любые числа, причем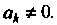 Обозначим многочлен от
Обозначим многочлен от
Матрицы Через
Через , тогда по определению
, тогда по определению

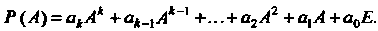 (5.7)
(5.7)
Из определения следует, что многочлен от матрицы можно получить, если в обычный многочлен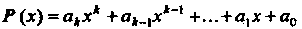 Вместо
Вместо Подставить
Подставить
Квадратную матрицу (и учесть, что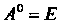 ).
).
Пусть дан многочлен , Если
, Если Является нулевой матрицей, т. е.
Является нулевой матрицей, т. е.
 То матрица
То матрица Называется корнем многочлена
Называется корнем многочлена , а многочлен
, а многочлен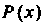
— аннулирующим многочленом для матрицы.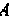 .
.
Пример 5.3. Найти произведение,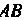 И
И Матриц
Матриц

Обе матрицы являются квадратными матрицамиодного и того же порядка (второго), поэтому можно получить произведения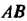 И
И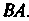 Применяя формулу
Применяя формулу
(5.6) для случая Получаем
Получаем
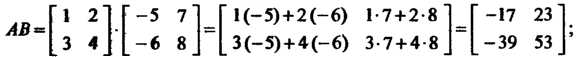
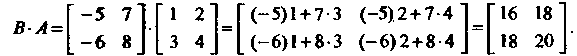
Отметим, что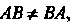 Т. е. результат умножения зависит от порядка множителей.
Т. е. результат умножения зависит от порядка множителей.
Пример S.4. Даны две матрицы
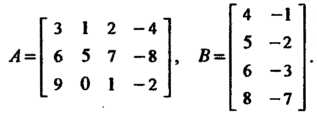
Найти произведение . Можно ли получить произведение
. Можно ли получить произведение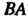 ?
?
Число столбцов матрицы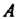 Равно числу строк матрицы
Равно числу строк матрицы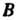 (ширина матрицы
(ширина матрицы равна высоте матрицы
равна высоте матрицы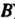 ), поэтому произведение
), поэтому произведение Определено. Умножая строку матрицы
Определено. Умножая строку матрицы На столбец матрицы
На столбец матрицы , по формуле (5.6) получаем
, по формуле (5.6) получаем
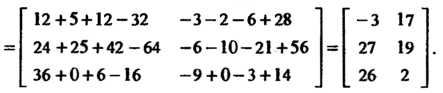
Произведение Не определено, так как число столбцов матрицы В не равно числу строк матрицы
Не определено, так как число столбцов матрицы В не равно числу строк матрицы .
.
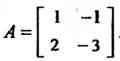

Пример 5.5. Найти многочлен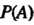 , если
, если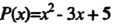 И
И
В соответствии с определением многочлена от матрицы (см. формулу (5.7)) получаем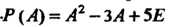 Или
Или
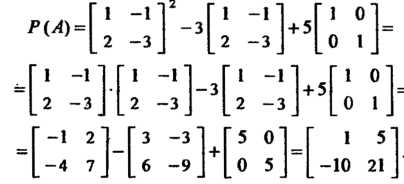
| < Предыдущая | Следующая > |
|---|