05.1. Матрицы. Осйовные определения

 

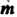Матрицей называется системаЧисел, расположенных в прямоугольной таблице изСтрок и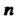Столбцов. Числа этой таблицы называются элементами матрицы. Обозначения матрицы:

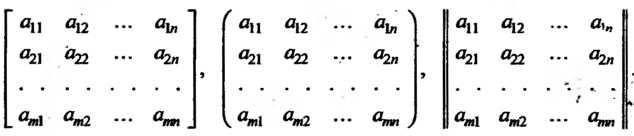
Элементы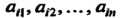СоставляютСтрокуЭлементы

СоставляютСтолбец- элемент, принад

ЛежащийСтроке иСтолбцу матрицы, числа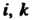Называют индексами элемента. Матрицу, имеющую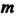Строк и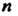Столбцов, называют матрицей размеров (читаетсяНа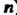). Употребляются и более краткие обозначения матрицы размеров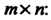

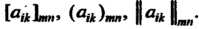
Матрицу обозначают также одной заглавной буквой, например

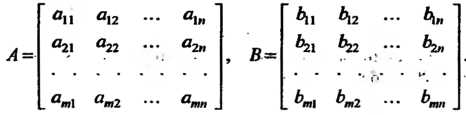
Если необходимо отметить, что матрица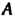Имеет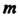Строк и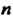Столбцов, т. е. необходимо указать ее размеры, то пишут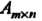Или

Две матрицыНазываются равными, если

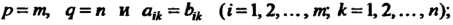Другими словами, если

Они одинаковых размеров и их соответствующие элементы равны.

Матрица, состоящая из одной строки, называется строчной матрицей, или матрицей-строкой. Строчная матрица имеет вид

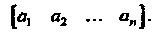
Матрица

Имеющая один столбец, называется столбцовой матрицей, или матрицей-столбцом.

Матрица, все элементы которой равны нулю, называется нулевой Нулевую матрицу обозначают буквой О.

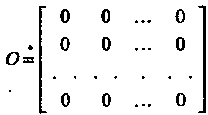
Квадратной называется матрица, у которой число строк равно числу столбцов 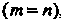, т. е. матрица вида

Порядком квадратной матрицы называется число ее строк.

Будем говорить, что элементыКвадратной матрицы образуют

Ее главную диагональ, а элементы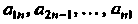- вторую диагональ.

Квадратная матрица называется симметрической, если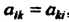, т. е. равны ее

Элементы, симметричные относительно главной диагонали.

Диагональной называется квадратная матрица, у которой все элементы, не принадлежащие главной диагонали, равны нулю, т. е. матрица

Скалярной называется диагональная матрица, у которо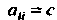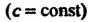й При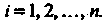

Единичной называется диагональная матрица, у которой все элементы главной диагонали равны единице. Единичную матрицу обозначают буквой Е:

Треугольной называется квадратная матрица, все элементы которой, расположенные по Одну сторону от главной диагонали, равны нулю. Различают соответственно верхнюю и нижнюю треугольные матрицы:

Матрица произвольных размеров вида

(5.1)

ГдеНазывается квазитреугольной (ступенчатой или

Трапециевидной).

Матрица, полученная из данной матрицы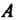Заменой каждой ее строки столбцом с тем же номером, называется транспонированной относительно. Если — матрица размером, то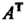Имеет размеры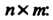

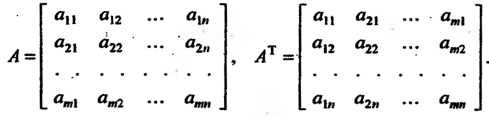
Например, если

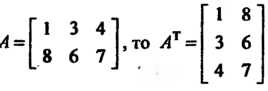
Элементарными преобразованиями матрицы называют следующие преобразования: 1) умножение строки (или столбца) матрицы на число, отличное от нуля; 2) прибавление к элементам строки (столбца) соответственных элементов другой строки (столбца), умноженных на любое число; 3) перестановка местами двух строк (столбцов).

Термин «матрица» был введен Д. Сильвестром в 1851 г.

< Предыдущая		Следующая >