04.10. Некоторые другие поверхности
В плоскости
Задана линия
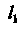Своими параметрическими уравнениями
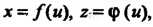(4.71)
Не пересекающая ось
Рассмотрим поверхность, полученную вращением этой л^нии вокруг оси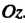
Параметрические уравнения рассматриваемой поверхности вращения Имеют вид
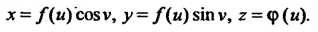(4.72)
Тор — поверхность, полученная вращением окружности вокруг оси, лежащей в плоскости данной окружности и не пересекающей ее. Эта поверхность напоминает спасательный круг, камеру автомобильной шины (рис. 4.22).
Рассмотрим тор, полученный вращением вокруг оси Oz окружности, заданной параметрическими уравнениями
Эта окружность лежит в плоскости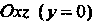
И определяется уравнениями вида
(4.71)| где
В соответствии с(4.72) получаем параметрические уравнения тора
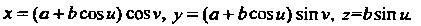(4.73)
Катеноид — поверхность, полученная вращением цепной линии вокруг ее оси (рис. 4.23). Рассмотрим катеноид, полученный вращением вокруг оси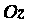
Цепной линии, заданной параметрическими уравнениями
Эта линия расположена в плоскости
(у = 0). Она определена уравнениями вида (4.71), где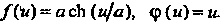
В соответствии с (4.72) находят
Параметрические уравнения катеноида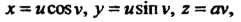 
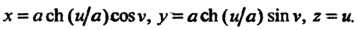Исключая из этих уравнений параметры
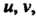Получаем
Катеноид является единственной минимальной поверхностью среди поверхностей вращения. Минимальные поверхности возникли при решении следующей задачи: среди всех поверхностей, проходящих через данную замкнутую пространственную линию, найти ту, которая имеет минимальную площадь поверхности, ограниченной данной линией. Отсюда происходит и название такой поверхности. Бельгийский физик Плато предложил простой экспериментальный способ получения минимальных поверхностей посредством мыльных пленок, натянутых иа проволочный каркас.
Катеноид обладает следующим свойством. Рассмотрим две окружности, полученные пересечением катеноида (4.74) соответственно плоскостями
Любая поверхность, края которой совпадают с этими окружностями, имеет площадь большую, чем часть катеноида, расположенная между указателей окружностями. Мыльная пленка, соединяющая данные окружности под действием сил внутреннего натяжения, принимает форму катеноида.
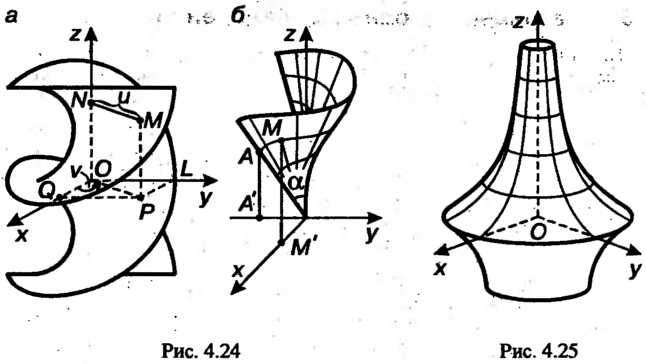
Геликоид - поверхность, описанная прямой, которая вращается с постоянной угловой скоростью вокруг неподвижной оси, пересекает ось под постоянным углом
И одновременно перемещается поступательно с постоянной скоростью вдоль этой оси. При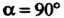
Геликоид называют прямым (рис. 4.24, а), при
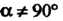Геликоид называют косым (рис. 4.24, б).
Рассмотрим прямой геликоид, описанный прямой, перпендикулярной оси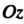
(см. рис. 4.24, а). Пусть
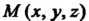- произвольная точка поверхности,
- ее
Проекция на плоскость
- проекции точки
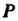Соответственно на оси
,
. Обозначим через
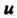Расстояние точки
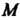До оси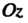
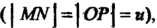А через
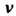- угол, образуемый отрезком
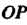С осью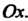
Параметрические уравнения геликоида имеют вид
Где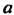
- некоторая постоянная.
Наглядное представление о положении отдельных прямых (лучей) при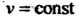 
Дают ступени винтойоЙ лестницы.
Представление о геликоиде можно составить, например, наблюдая движение г винта вертолета при его вертикальном взлете. Отметим, что первоначально вертолеты называли геликоптерами..винтокрылыми. Первый эскиз i е. шкоида был нарисован еще Леонардо да Винчи.
Разнообразные геликоиды широко применяются на пракч икс )то объясняется ' следующим: геликоид образован сложением двух самых распространенных видов
97
4 Зак. 1
Равномерного движения - прямолинейного и вращательного. Вследствие этого геликоид можно применить там, где необходимо перейти от одного из указанных видов движения к другому, что имеет место практически в любой машине.
Псевдосфера - поверхность, полученная вращением трактрисы вокруг ее асимптоты (рис. 4.25). Рассмотрим псевдосферу, полученную вращением вокруг оси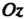
Трактрисы
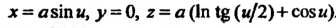
Эта трактриса лежит в плоскости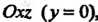
Ось
Служит ее асимптотой. Ли
Ния задана параметрическими уравнениями вида (4.71), гд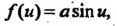е
В соответствии с (4.72) получены параметрические
Уравнения псевдосферы
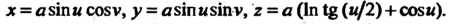
Важность псевдосферы состоит в том, что на ней частично реализуется плоская неевклидова геометрия Лобачевского. Этот удивительный факт установил итальянский математик Эудженио Бельтрами в 1868 г., уже после смерти Н. И. Лобачевского.
II
| < Предыдущая | Следующая > |
|---|
