04.09. Поверхности второго порядка
Поверхностью второго порядка называется поверхность, определяемая алгебраическим уравнением второй степени относительно текущих координат х, у, z.
Канонические уравнения поверхностей второго порядка:
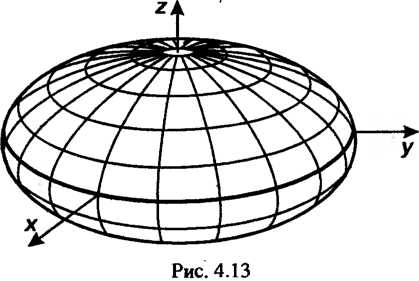
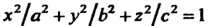 . (эллипсоид, рис. 4.13); (4.51)
. (эллипсоид, рис. 4.13); (4.51)
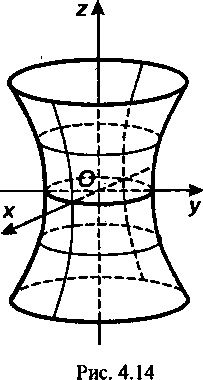
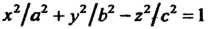 (однополосный гиперболоид, рис. 4.14); (4.52)
(однополосный гиперболоид, рис. 4.14); (4.52)
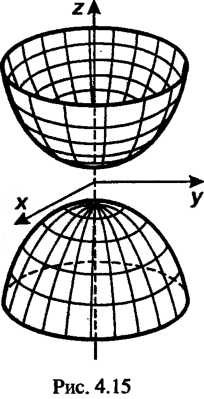
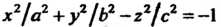 (двуполостный гиперболоид, рис 4.15); (4.53)
(двуполостный гиперболоид, рис 4.15); (4.53)
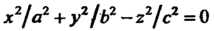 '(конус, рис. 4.16); (4.54)
'(конус, рис. 4.16); (4.54)
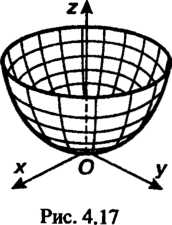
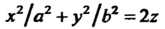 (эллиптический параболоид, рис. 4.17); (4.55)
(эллиптический параболоид, рис. 4.17); (4.55)
(эллиптический цилиндр, рис. 4.19); (4.57)
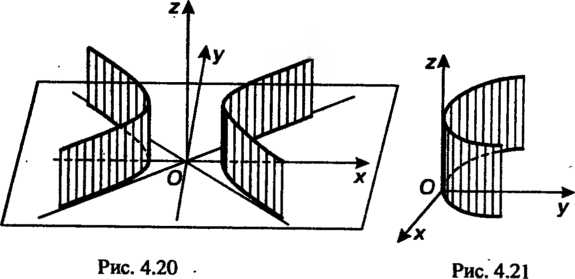
(гиперболический цилийдр, рис. 4.2Q); (4.58)


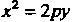
(параболический цилиндр, рис. 4:21); (4.59)
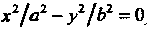
(пара пересекающихся плоскостей); (4.60)

(пара параллельных плоскостей); (4.61)
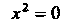
(пара совпадающих плоскостей). (4.62)


Замечание, 1. Уравнение (4.51) при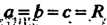 Принимает вид
Принимает вид
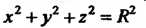 Г. -5. .. (4.63)
Г. -5. .. (4.63)
И ^определяет сферу рад^сё С центром-в начале Координат.' -
С центром-в начале Координат.' -
Общее уравнение' второй степени относительно Меняет бытьприведейо к одному из уравнений (4.51) - (4.63) или к одному из следующих уравнений:
Меняет бытьприведейо к одному из уравнений (4.51) - (4.63) или к одному из следующих уравнений:
(4.64)
•г :Ki. JC-- •: ' l(445)
I!7 (4.66)
• ' :^7) •
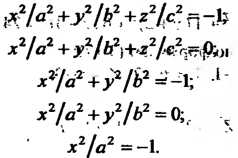 (4.68)
(4.68)
Уравнениям (4.64), (4.66) и (4.68) не удовлетворяют координаты ни одной точки пространства; уравнению (4.65) удовлетворяют координаты единственной точки Уравнению (4.67) удовлетворяют координаты точек, лежащих на
Уравнению (4.67) удовлетворяют координаты точек, лежащих на
Прямой
3 ам е ч а ни е 2. Если уравнение
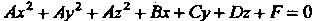 (4.69)
(4.69)
(т. е. уравнение, у которого коэффициенты при квадратах координат равны между собой, а коэффициенты при произведениях координат равны нулю) определяет некоторую поверхность, то этой поверхностью является сфера Уравнение (4.69) в этом случае может быть приведено к виду
 (4.70)
(4.70)
Уравнение (4.70) является уравнением сферы радиуса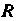 С центром в точке
С центром в точке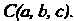
Прямые, целиком лежащие на некоторой поверхности, называются прямолинейными образующими данной поверхности.
Однополосный гиперболоид (4.52) имеет два семейства прямолинейных образующих:
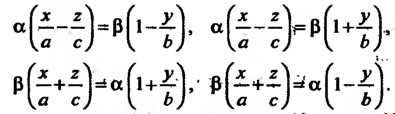
Гиперболический параболоид (4.56) также имеет два семейства прямолинейных образующих:

Пример 4.24. Определить вид и параметры поверхности второго порядка, заданной уравнением
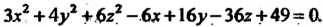
Преобразуем это уравнение, выделив в левой части полные квадраты:

Введем новые координаты по формулам (3.17):
Тогда уравнение примет ввд
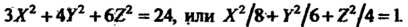
Полученное уравнение определяет эллипсоид (см. (4.51)), для которого
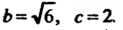 Центр эллипсоида находится в точке
Центр эллипсоида находится в точке В новой системе
В новой системе
Координат центром является точка с координатами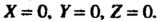 Из этих ра
Из этих ра
Венств и формул (I) находим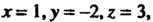 Т. е. координаты точки
Т. е. координаты точки
Пример 4.25. Определить вид и параметры поверхности
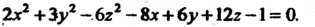
Преобразуем это уравнение:
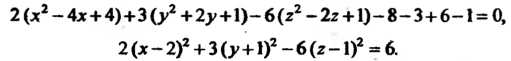
Переходя к новым координатам по формулам Полу
Полу
Чаем
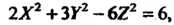 Или
Или
Это уравнение определяет однополостный гиперболоид (см. (4.52)), для которого  С центром в точке
С центром в точке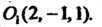
Пример 4.26. Доказать, что уравнение Определяет гиперболиче
Определяет гиперболиче
Ский параболоид.
Введем новые координаты по формулам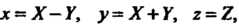 Тогда
Тогда
Уравнение примет вид
Полученное уравнение является уравнением вида (4.56), для которого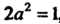 ,
,
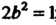 ; оно определяет гиперболический параболоид.
; оно определяет гиперболический параболоид.
Пример 4.27. Доказать что уравнение Определяет конус.
Определяет конус.
Переходя к новым координатам по формулам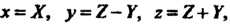 По
По
Лучаем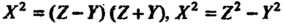 , или
, или
Полученное уравнение является уравнением вида (4.54), для которого 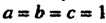 , оно определяет конус.
, оно определяет конус.
| < Предыдущая | Следующая > |
|---|
