04.08. Цилиндрические поверхности. Поверхности вращения
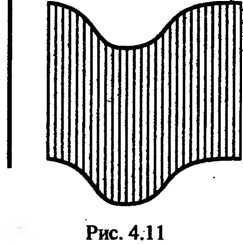
Цилиндрической называется поверхность, описываемая прямой (образующей), движущейся вдоль некоторой линии (направляющей) и остающейся параллельной исходному направлению (рис. 4.11). Уравнение цилиндрической поверхности, образующие которой параллельны оси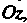 Имеет вид
Имеет вид
Особенность уравнения (4.48) состоит в том, что оно не содержит переменной Есяи уравнение
Есяи уравнение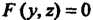 Определяет некоторую поверхность, то ею является
Определяет некоторую поверхность, то ею является
Цилиндрическая поверхность с образующей, параллельной оси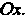 Если уравнение
Если уравнение 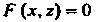 Определяет некоторую поверхность, то ею является цилиндрическая
Определяет некоторую поверхность, то ею является цилиндрическая
Поверхность с образующей, параллельной оси Поверхность, образованная вращением линии
Поверхность, образованная вращением линии
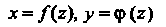 (4.49)
(4.49)
Вокруг оси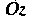 (рис. 4.12), определяется уравнением
(рис. 4.12), определяется уравнением
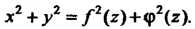 (4.50)
(4.50)
Поверхность, образованная вращением линии Вокруг оси
Вокруг оси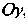 ,
,
Имеет уравнение
Поверхность, образованная вращением линии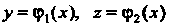 Вокруг оси
Вокруг оси
Ох, определяется уравнением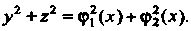
. Поверхностью вращения второго порядка называется поверхность, полученная вращением линии второго порядка вокруг ее оси.
Эллипсоидом вращения называется поверхность, полученная вращением эллипса вокруг одной из его осей. Уравнение эллипсоида вращения, полученного вращением эллипса Вокруг оси
Вокруг оси , имеет вид
, имеет вид 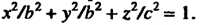
Однополосным гиперболоидом вращения называется поверхность, полученная вращением гиперболы вокруг ее мнимой оси. Однополосный гиперболоид вращения, полученный вращением гиперболы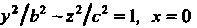 Вокруг оси
Вокруг оси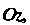 Имеет уравнение
Имеет уравнение

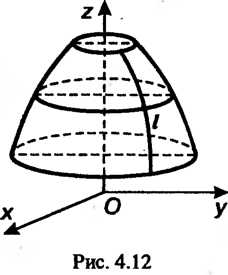
Двуполостным гиперболоидом вращения называется поверхность, полученная вращением гиперболы вокруг ее действительной оси. Двуполо-стный гиперболоид, полученный вращением гиперболы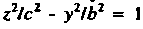 ,
,
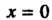 Вокруг оси
Вокруг оси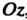 , определяется уравнением
, определяется уравнением

Параболоидом вращения'называется поверхность, полученная вращением параболы вокруг ее оси. Уравнение параболоида вращения, полученного вращением параболы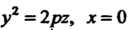 Вокруг оси
Вокруг оси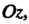 Имеет вид
Имеет вид
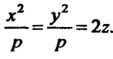
• Пример 4.23. Составить уравнение поверхности, полученной вращением линии.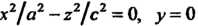 Вокруг оси
Вокруг оси
Данные уравнения определяют пару пересекающихся прямых в плоскости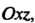 проходящих через начало координат (являющихся пересечением плоскостей
проходящих через начало координат (являющихся пересечением плоскостей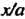
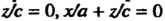 С плоскостью
С плоскостью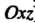 ). Приведем эти уравнения к виду (4.49):
). Приведем эти уравнения к виду (4.49):
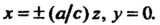
В соответствии с уравнением (4.50) получаем
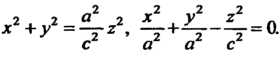
Последнее уравнение является уравнением конуса вращения, получающегося при вращении указанных прямых вокруг оси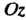
| < Предыдущая | Следующая > |
|---|