04.07. Задачи на прямую и плоскость

 

Прямая как линия пересечения двух плоскостей. Рассмотрим две плоскости, заданные общими уравнениями (4.22) и (4.23). Если условие (4.24) не выполнено (т. е. коэффициенты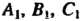Не пропорциональны коэффициентам , то плоскости пересекаются по прямой, определяемой уравнениями

(4.37)

Эти уравнения приводятся к параметрическому виду

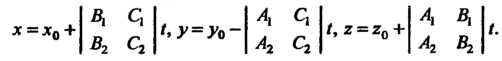
(4.38)

(4.39)

Где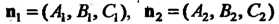- нормальные векторы данных плоскостей.

ТочкаНа прямой может быть выбрана произвольно; для этого не

Обходимо в системе (4.37) зафиксировать значение одной переменной (например, 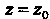), из полученной системы уравнений найти значения двух других переменных ().

Пучок плоскостей — множество всех плоскостей, проходящих через одну и ту же прямую. Уравнение пучка плоскостей, проходящих через прямую (4.37), имеет вид

Где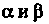— любые действительные числа, причем хотя бы одно из них отлично от нуля. Это уравнение можно привести к вицу

(4.40)

ГдеУравнение (4.40) определяет все плоскости пучка, за исклю

Чением той, которой соответствует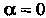, т. е. за исключением плоскости

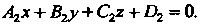
Данная прямая имеет направляющий вектор

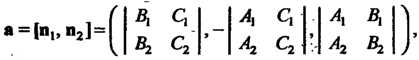
Угол между прямой и плоскостью. Синус угла между прямой

(4.41)

И плоскостью

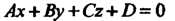(4.42)

Определяется формулой

(4.43)

Взаимное расположение прямой й плоскости. Прямая (4.41) и плоскость

(4.42) пересекаются, если

(4.44)

Перпендикулярны, когда

(4.45)

Параллельны, если

(4.46)

Совпадают, когда

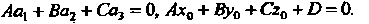(4.47)

Координаты точки пересечения прямой (4.41) и плоскости (4.42) находятся из системы их уравнений.

Неравенство (4.44) означает, что нормальный вектор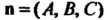Плоскости

(4.42) и направляющий вектор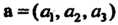Прямой (4.41) не перпендикулярны,

Т. е. прямая и плоскость не параллельны.

Равенства (4.43) означают, что векторы п и а коллинеарны, т. е. прямая (4.41) и плоскость (4.42) перпендикулярны.

Соотношения (4.46) показывают, что векторып и а перпендикулярны, т. е. прямая и плоскость параллельны, но точкаПрямой (4.41) не при

Надлежит плоскости (4.42).

Равенства (4.47) означают, что векторыИПерпендикулярны и точка 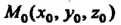Прямой принадлежит плоскости (прямая лежит в плоскости). Пример 4.19. Уравнения прямой 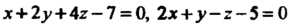привести к параметрическому виду.

Поскольку в этих уравнениях коэффициенты при текущих координатах непропорциональны, то плоскости, определяемые данными уравнениями, пересекаются. Данные уравнения определяют прямую. Выберем на прямой точку. Полагая в этих уравнениях, например,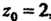, получаем

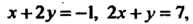
Откуда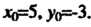На прямой зафиксирована точка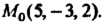По формуле (4.39)

Найдем направляющий вектор прямой. Так как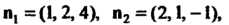То

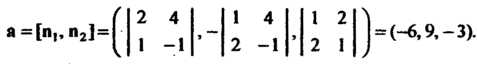
Параметрические уравнения (4.38) данной прямой принимают вид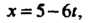

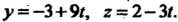
Замечание. В качестве направляющего вектора можно взять 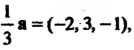Тогда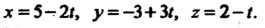

Пример 4.20.' Найти угол между прямой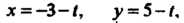 И плоскостью

Применяя формулу (4.43) Для случая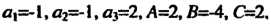Находим

Пример 4.21. Найти проекцию точки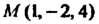На плоскость

Этой проекцией является точка пересечения перпендикуляра к плоскости, проходящей через точку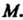Для прямой, перпендикулярной плоскости, направляющим вектором будет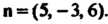Параметрические уравнения прямой, перпендикулярной плоскости и проходящей через точку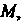Примут вид

Подставляя эти выражения в уравнение плоскости, находим:

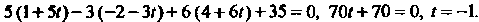
При этом значении t из уравнений прямой получаем: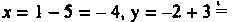

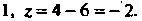Следовательно, точка— искомая проекция.

Пример 4.22. Вершины пирамиды находятся в точках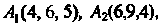

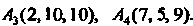Найта: 1) длину ребра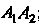; 2) угол между ребрам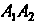иИ 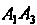; 3) площадь грани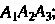; 4) объем пирамиды; 5) уравнение плоскости

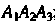; 6) уравнения прямой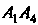; 7) угол между ребром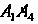И гранью;

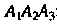8) уравнения высоты, опущенной из вершины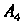На грань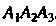

Найдем сначала координаты векторовИ координаты век

Торного произведения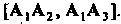По формуле (3.15) получаем

С помощью формулы (3.26) находим

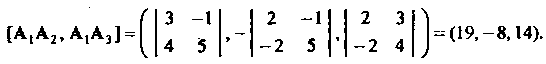
1.  Длина ребра АХА2 равна расстоянию между точкамиКоторое вычислим по формуле (1.26):

Тот же результат можно получить, найдя модуль вектора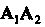По формуле (3.11).

2.  Угол между ребрам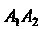иИРавен углуМежду векторами

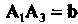. В соответствии с формулой (3.22) получаем

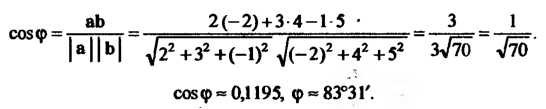
3. Площадь грани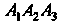Равна площади треугольникаКоторую вы

Числим по формуле (3.29), использовав формулу (3.11) для модуля вектора и координаты вектора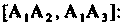

4. Объем пирамидыНайдем по формуле (3.35):

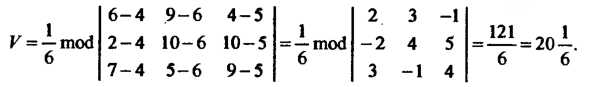
5. Уравнение плоскости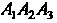Как плоскости, проходящей через три точки

(см. (4.14)), принимает вид

(I)

6. Уравнения прямойКак прямой, проходящей через две точки

(см. (4.21)), запишутся так:

(II)

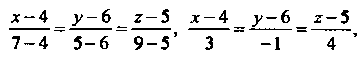
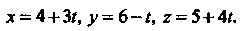
7. Угол между ребромИ граньюРавен углу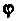Между плоскостью

(I) и прямой (II). По формуле (4.43) находим

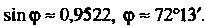
Или

 

8. Уравнения высоты, опущенной из вершины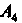На грань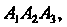Можно за

Писать как уравнения прямой, проходящей через точку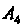И перпендикулярной плоскости (I), имеющей нормальный вектор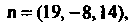Который для этой

Прямой будет направляющим вектором. Уравнения (4.19) в данном случае принимают вид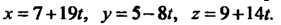

< Предыдущая		Следующая >