04.06. Задачи, относящиеся к прямым в пространстве

Угол между двумя прямыми. угол между направляющими векторами этих прямыми. Косинус угла между двумя прямыми

(4.29)

F* »**>’ .  .1 'iliei-i’-dt* it t'  l: “it i

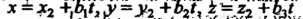
(4.3,0)

"i

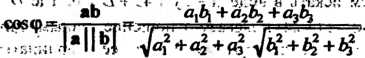
(4-Й)

Равенство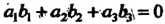Выражает необходимое и достаточное условие

Перпендикулярности прямых (4.29), (4.30). Необходимое и достаточное условие параллельности этих прямых выражается равенствами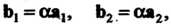 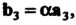Или

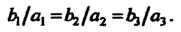
(4.32)

Взаимное расположение двух прямых в пространстве. Для исследования взаимного расположения прямых (4.29) и(4.30) рассматривается смешанное произведение трех векторов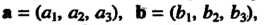

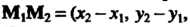
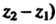. Бели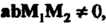Т. е.

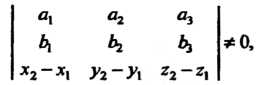
То прямые являются скрещивающимися. Неравенство (4.33) означает, что векторы 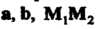Некомпланарны.'

 

(4.33)

 

Прямые (4.29) и (4.30) лежат в одной плоскости тогда и только тогда, когда 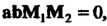Т. е.  1

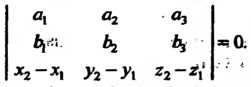
(4-34)

Этипрямые пересекаются, если первые две строки определителя не пропори циональны, т, е. не выполнено. условие (4.32). Прямые параллельны, когда первые две строки определителя пропорциональны. Прямые совпадают, если пропорцио-

Нальны все строки определителя (4.34).  ¦:

Замечание. Чтобы найти точку пересечения прямых (4.29) и

(4.30), необходимо решить систему их уравнений; при этом целесообразно параметры обозначить различными _ буквами (так как одна и та же точка пересечения прямых получается, как правило, при различных значениях параметра в уравнениях данных прямых).

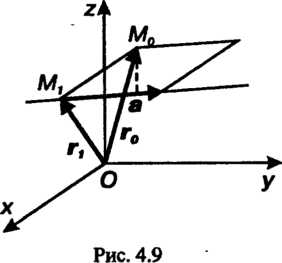
(4.35)

Где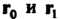- радиусы-векторы точек,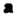- направляющий вектор пря

Мой (рис. 4.9).

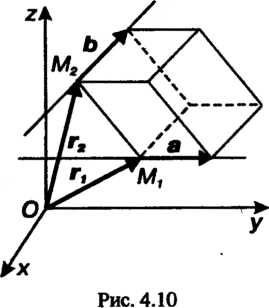
Расстояние между двумя прямыми. Кратчайшее расстояние между двумя прямыми (4.29) и (4.30) определяется формулой

(4.36)

Где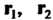- радиусы-векторы точек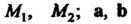— направляющие векторы

Данных прямых (рис. 4.10).

Пример 4.16. Найти угол между двумя прямыми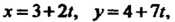

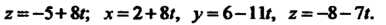
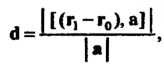
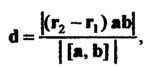
Первая прямая имеет направляющий вектор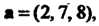Вторая -

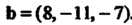. По формуле (4.31) находим

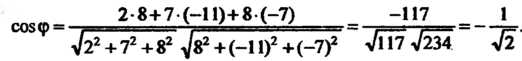
Следовательно,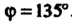

Пример 4.17. Доказать, что прямые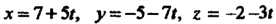И

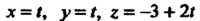Пересекаются. Найти точку их пересечения.

Рассмотрим векторы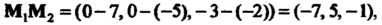

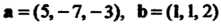И их смешанное произведение

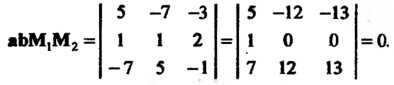
Поскольку смешанное произведение трех векторов равно нулю, то векторы компланарны; значит, данные прямые лежат в одной плоскости. Так как направляющие векторыЭтих прямых неколлинеарны (их координаты не пропорциональны), то прямые пересекаются.

Чтобы найти точку пересечения, приравняем выражения для координат, предварительно обозначив параметр буквойВ уравнениях второй прямой:

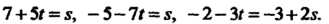
Из первых двух уравнений следует, что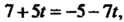Откуда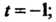Следова

Тельно,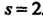. При этих значениях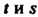Третье уравнение обращается в тождество. Подставляя значение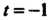В уравнения первой прямой (или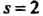В уравнения

Второй прямой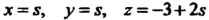), находим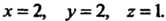Итак,

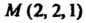- точка пересечения данных прямых.

Пример 4.18. Найти расстояние от точки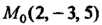До прямой:

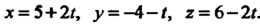
Найдем сначала векторное произведение, входящее в формулу (4.35):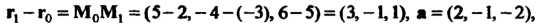

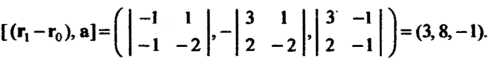
По формуле (4.35) получаем

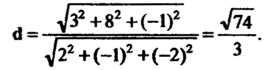
< Предыдущая		Следующая >