04.05. Задачи, относящиеся к плоскостям

 

Взаимное расположение двух плоскостей. Даны две плоскости

(4.22)

(4.23)

Необходимое и достаточное условие параллельности этих плоскостей выражается равенствами

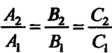
(4.24)

А их совпадения — равенствами

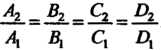(4.25)

Другими словами, плоскости параллельны тогда и только тогда, когда пропорциональны их коэффициенты при текущих координатах; например, плоскости

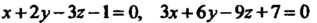Параллельны. Плоскости совпадают тогда и только тогда, когда пропорциональны коэффициенты при текущих координатах и свободные члены; например, плоскости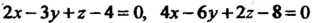Совпадают. Если условие (4.24) не выполняется, то плоскости (4.22) и (4.23) пересекаются. Угол между двумя плоскостями. Косинус угла между плоскостями (4.22). и

(4.23)  определяется формулой

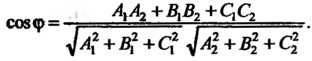(4.26)

Необходимое и достаточное условие перпендикулярности плоскостей (4.22) и

(4.23)  выражается равенством

(4.28)

Пример 4.12. Составить уравнение плоскости, проходящей через точку 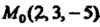И параллельной плоскости 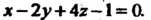Это уравнение будем искать в ви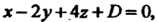деГде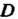- неизвестный

Свободный член (в формуле (4.24) полагаем отношение равным единице).

Так как плоскость проходит через точку, то ее координаты должны удов-

Летворять последнему уравнению: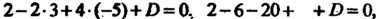

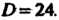Следовательно,- искомое у равнение.

Пример 4.13. Найти угол между двумя плоскостями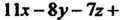

Косинус угла найдем по формуле (4.26), подставив в нее значения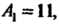

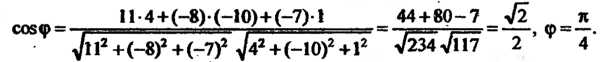
Пример 4.14. Вычислить расстояние от точки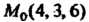До плоскости

Подставив в формулу (4.28) значения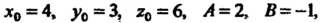 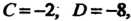Получим

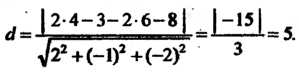
Пример 4.15. Найти расстояние между параллельными плоскостями

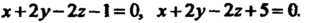
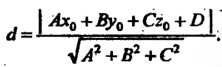
Это расстояние равно расстоянию любой точки одной плоскости до другой. Выберем на первой плоскости произвольную точку. Приняв, например, что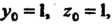Из уравненияНайдемПо формуле

(4.28) находим расстояние от точкиДо плоскости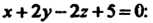

< Предыдущая		Следующая >