04.03. Различные виды уравнения плоскости
Плоскость в пространстве можно задать различными способами (точкой и век-тором, перпендикулярном плоскости, тремя точками и т. д.), в зависимости от этого рассматривают различные виды ее уравнения.
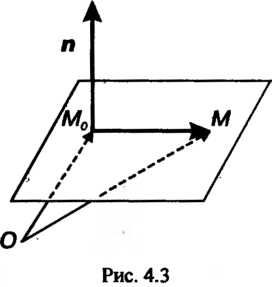
Уравнение плоскости, проходящей через данную точку и перпендикулярной данному вектору. Ненулевой вектор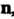 , перпендикулярный плоскости, называют ее нормальным вектором. Если дана точка
, перпендикулярный плоскости, называют ее нормальным вектором. Если дана точка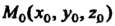 И нормальный вектор
И нормальный вектор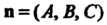 Плоскости, то ее уравнение имеет вид
Плоскости, то ее уравнение имеет вид
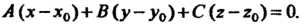 (4.9)
(4.9)
В этом уравнении коэффициенты А, В, С являются координатами нормального вектора Равенство (4.9) выражает необходимое и достаточное условие перпендикулярности двух векторов: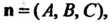
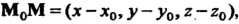 Где
Где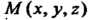
- любая точка плоскости (рис. 4.3).
Общее уравнение плоскости. Уравнение первой степени относительно декартовых координат
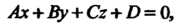 (4.10)
(4.10)
Где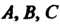 Одновременно в нуль не обращаются, т. е.
Одновременно в нуль не обращаются, т. е.
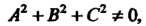 (4.11)
(4.11)
Определяет плоскость в пространстве. Уравнение (4.10) называется общим уравнением плоскости. Отметим частные случаи этого уравнения.
Если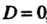 , то уравнение (4.10) принимает вид
, то уравнение (4.10) принимает вид
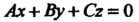
И определяет плоскость, проходящую через начало координат (рис. 4.4, а; координаты _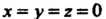 Удовлетворяют данному уравнению). ?
Удовлетворяют данному уравнению). ?
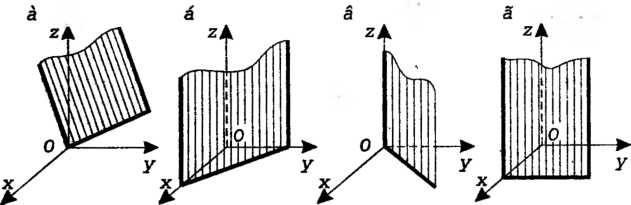
Если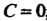 , то уравнение (4.10) принимает вид
, то уравнение (4.10) принимает вид
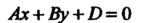
Н определяет плоскость, параллельную оси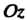 (рис. 4.4, б); нормальный вектор
(рис. 4.4, б); нормальный вектор 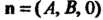 Перпендикулярен оси
Перпендикулярен оси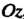 , ибо
, ибо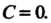
Если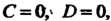 То уравнение (4.10) принимает вид
То уравнение (4.10) принимает вид
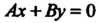
И определяет плоскость, проходящую через ось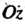 (рис. 4.4, в; плоскость параллельна оси
(рис. 4.4, в; плоскость параллельна оси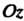 И проходит через начало координат; в этом случае
И проходит через начало координат; в этом случае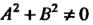 В силу условия (4.11)).
В силу условия (4.11)).
Если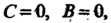 То уравнение (4.10) принимает вид
То уравнение (4.10) принимает вид
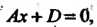 Или
Или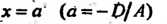
И определяет плоскость, параллельную плоскости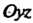 Или перпендикулярную оси Ох (рис. 4.4, г; нормальный вектор
Или перпендикулярную оси Ох (рис. 4.4, г; нормальный вектор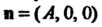 Перпендикулярен плоскости
Перпендикулярен плоскости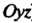 ).
).
Если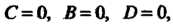 То уравнение (4.10) принимает вид
То уравнение (4.10) принимает вид
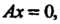 Или
Или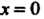 (так как
(так как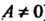 )
)
И определяет координатную плоскость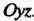
Замечание. Если в уравнении (4.10) свободный член равен нулю (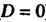 ), то плоскость проходит через начало координат; если коэффициент прн одной из текущих координат равен нулю, то плоскость параллельна соответствующей координатной оси (например, если
), то плоскость проходит через начало координат; если коэффициент прн одной из текущих координат равен нулю, то плоскость параллельна соответствующей координатной оси (например, если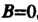 , то плоскость параллельна оси
, то плоскость параллельна оси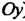 ); еелк в нуль обращаются свободный член и один из коэффициентов при текущей координате, то плоскость проходит через соответствующую ось (если
); еелк в нуль обращаются свободный член и один из коэффициентов при текущей координате, то плоскость проходит через соответствующую ось (если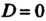 Н
Н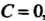 , то плоскость
, то плоскость
Проходит через ось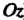 ); если равны нулю два коэффициента при текущих координатах, то плоскость параллельна соответствующей координатной плоскости (когда
); если равны нулю два коэффициента при текущих координатах, то плоскость параллельна соответствующей координатной плоскости (когда 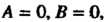 Плоскость параллельна шЮскостн
Плоскость параллельна шЮскостн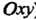 ); если обращаются в нуль свободный член и два коэффициента при текущих координатах, то плоскость совпадает с соответствующей координатной плоскостью (когда
); если обращаются в нуль свободный член и два коэффициента при текущих координатах, то плоскость совпадает с соответствующей координатной плоскостью (когда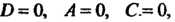 плоскость совпадает с плоскостью <
плоскость совпадает с плоскостью <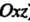 ).
).
Уравнение плоскости в отрезках, отсекаемых на осях координат. Если все коэффициенты уравнения (4.10) и его свободный член отличны от нуля, то уравнение можно привести к виду
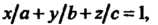 (4.12)
(4.12)
Где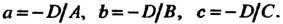 Числа
Числа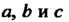 Означают величины направ-
Означают величины направ-
Ленных отрезков, отсекаемых на осях координат. Этим объясняется название данного вида уравнения плоскости.
Нормальное уравнение плоскости. Уравнение
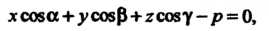
(4.13)
Где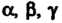 - углы, образованные нормальным вектором плоскости с координат
- углы, образованные нормальным вектором плоскости с координат
Ными осями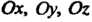 Соответственно,
Соответственно,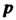 - длина перпендикуляра, опушенного
- длина перпендикуляра, опушенного
Из начала координат на плоскость, называется нормальным (или нормированным) уравнением плоскости. Чтобы привести общее уравнение плоскости к виду (4.13), необходимо умножить его на нормирующий множитель
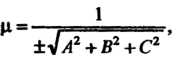
Где знак выбирается противоположным знаку После умножения уравнения
После умножения уравнения
(4.10) на число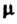 Получаем нормированное уравнение плоскости
Получаем нормированное уравнение плоскости
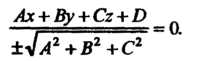
Уравнение плоскости, проходящей через три точки. Если даны три точки
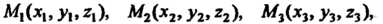 Не лежащие на одной прямой, то уравнение плоскости, проходящей через эти точки, имеет вид
Не лежащие на одной прямой, то уравнение плоскости, проходящей через эти точки, имеет вид
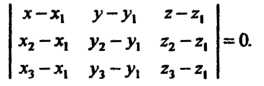
(4.14)
Равенство (4.14) выражает необходимое и достаточное условие (см. (3.36)) компланарности трех векторов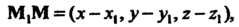
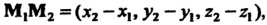
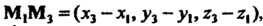 Где
Где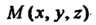
— любая точка данной плоскости (рис. 4.5).
Уравнение плоскости, проходящей через две точки и параллельной данному вектору. Если задан вектор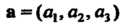 И две точки
И две точки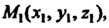
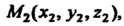 Причем векторы
Причем векторы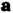 И
И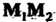 . неколлицеарны (рис. 4.6), то уравне-
. неколлицеарны (рис. 4.6), то уравне-
Ние плоскости, проходящей через эту точку параллельно вектору а, имеет вид
(4-15)
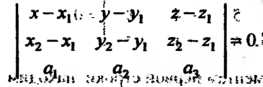
Равенство (4.15) выражает необходимое и достаточное, условие компланарности трех векторов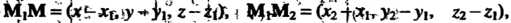
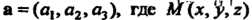 - любая точка данной rmoikOtm
- любая точка данной rmoikOtm
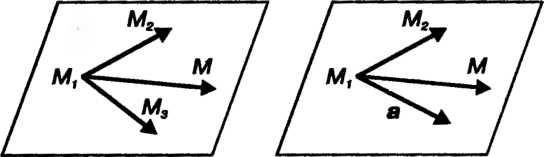
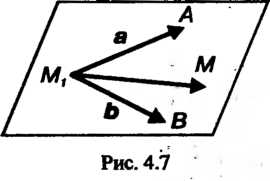
Уравнение плоскости, проходящей через данную точку и параллельной двум неколлннеарным векторам. Бели даны два неколлинеарных вектора (рис. 4.7)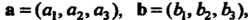 И точка
И точка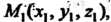 : то уравнение плос
: то уравнение плос
Кости, проходящей через данную точку параллельно векторам а и Ь, имеет вид
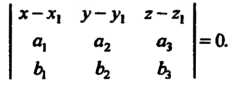
(4.16)
Равенство (4.16) выражает необходимое и достаточное условие компланарности трех векторов: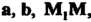 Где
Где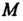 - произвольная точка данной плоскости.
- произвольная точка данной плоскости.
Параметрические уравнения плоскости. Если даны два неколлинеарных вектора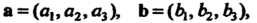 И точка
И точка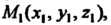 То параметрические уравнения плоскости, проходящей через эту точку параллельно данным векторам, имеют вид
То параметрические уравнения плоскости, проходящей через эту точку параллельно данным векторам, имеют вид
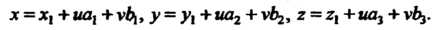
(4-17)
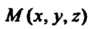
Уравнения (4.17) следуют из равенства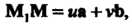 Где -
Где -
Любая точка плоскости (равенство
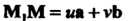 Означает, что любой вектор
Означает, что любой вектор
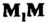 Можно разложить по векторам
Можно разложить по векторам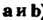 ).
).
Пример 4.6. Записать уравнение плоскости,. проходящей через точку 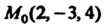 И имеющей нормальный вектор
И имеющей нормальный вектор
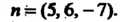
Так как в данном случае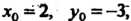
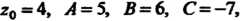 То уравнение (4.9) принимает вид
То уравнение (4.9) принимает вид
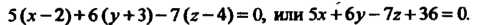
Пример 4.7. Составить уравнение плоскости, проходящей через точку 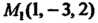 Параллельно векторам
Параллельно векторам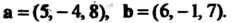 Данные векторы неколлинеарны, так как их координаты не пропорциональны.
Данные векторы неколлинеарны, так как их координаты не пропорциональны.
В соответствии с уравнением (4.16) получаем
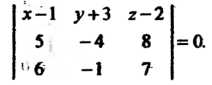
Разлагая определитель по элементам первой строки, находим
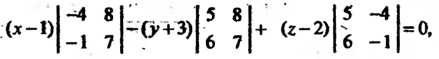
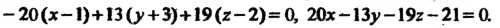
Пример 4.8. Найти величины отрезков, отсекаемых на осях координат плоскостью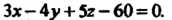
Разделив обе части уравнения на 60 и преобразовав его, получим
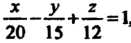 , или
, или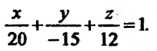
Сравнивая последнее уравнение с уравнением (4.12), заключаем, что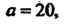
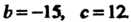 Таковы величины отрезков, отсекаемых плоскостью соответственно на осях
Таковы величины отрезков, отсекаемых плоскостью соответственно на осях
Пример 4.9. Составить уравнение плоскости, проходящей через три
Точки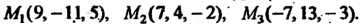
В соответствии с уравнением (4.14) получаем
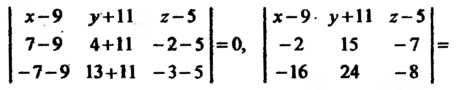
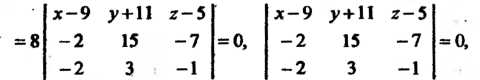
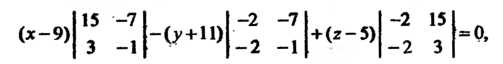
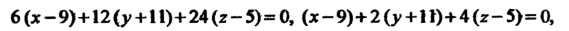
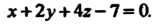
| < Предыдущая | Следующая > |
|---|