04.02. Параметрические уравнения линии и поверхности
Параметрическими уравнениями линии в пространстве называются уравнения вида
 (4.5)
(4.5)
Где — функции некоторой переменной
— функции некоторой переменной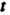 (параметра), если
(параметра), если
При каждом значении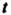 Из конечного или бесконечного промежутка они дают координаты всех точек данной линии и только таких точек.
Из конечного или бесконечного промежутка они дают координаты всех точек данной линии и только таких точек.
Параметрические уравнения часто применяются в механике для описания траектории движущейся точки, роль параметра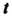 В таких случаях играет время. Параметрическими уравнениями поверхности называются уравнения вида
В таких случаях играет время. Параметрическими уравнениями поверхности называются уравнения вида
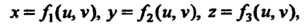 (4.6)
(4.6)
Где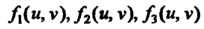 - функции двух переменных
- функции двух переменных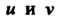 (параметров),
(параметров),
Если при любых значениях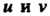 (меняющихся в некоторой области) они дают координаты всех точек данной поверхности и только таких точек.
(меняющихся в некоторой области) они дают координаты всех точек данной поверхности и только таких точек.
Правые части уравнений (4.6) содержат два параметра, а уравнения (4.5)-только один параметр.
Пример 4.4. Составить параметрические уравнения винтовой линии.
Винтовой линией называется линия, описываемая точкой, равномерно движущейся по образующей кругового цилиндра, который при этом вращается вокруг своей оси с постоянной угловой скоростью.
Выберем ось вращения цилиндра в качестве оси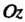 Декартовой прямоугольной системы координат в пространстве (рис. 4.1). Обозначим через v постоянную скорость прямолинейного движения точки вдоль образующей,
Декартовой прямоугольной системы координат в пространстве (рис. 4.1). Обозначим через v постоянную скорость прямолинейного движения точки вдоль образующей,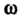 - скорость вращательного движения,
- скорость вращательного движения,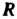 - радиус цилиндра. Пусть в начальный момент точка находилась га осн
- радиус цилиндра. Пусть в начальный момент точка находилась га осн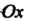 (совпадала с точкой
(совпадала с точкой ), а в момент времени
), а в момент времени - в положении
- в положении Обозначим буквой
Обозначим буквой Проекцию точки
Проекцию точки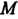 На плоскость
На плоскость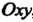 , буквой
, буквой — проекцию точки
— проекцию точки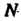 На ось
На ось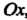 . буквой
. буквой - проекцию точки
- проекцию точки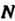 На ось
На ось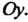 Обозначим через
Обозначим через угол между
угол между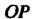 И
И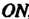 , получаем
, получаем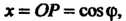
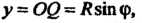
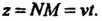 Поскольку
Поскольку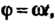 То
То
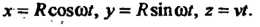
(4.7)
Уравнения (4.7) являются параметрическими уравнениями винтовой линии.
Пример 4.5. Составить параметрические уравнения сферы радиуса R.
Введем в рассмотрение систему декартовых прямоугольных координат с началом в центре сферы и систему сферических координат с началом в той же точке (рис. 4.2). Пусть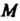 — произвольная точка сферы,
— произвольная точка сферы, - ее проекция на плоскость
- ее проекция на плоскость 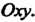 Обозначим угол, образуемый вектором
Обозначим угол, образуемый вектором С осью
С осью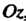 , через
, через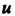 (широта); угол, образуемый вектором
(широта); угол, образуемый вектором С осью
С осью , через
, через (долгота). Принимая во внимание определение декартовых координат (или связь межау декартовыми и сфериче-
(долгота). Принимая во внимание определение декартовых координат (или связь межау декартовыми и сфериче-

Скими координатами, см. 1.13, формулы (1.29)), получаем параметрические уравнения сферы
 (4.8)
(4.8)
Где
Исключив из этих уравнений параметры (для чего нужно возвести в квадрат обе части каждого уравнения и почленно сложить), получим уравнение сферы (4.4).
(для чего нужно возвести в квадрат обе части каждого уравнения и почленно сложить), получим уравнение сферы (4.4).
| < Предыдущая | Следующая > |
|---|