04.01. Уравнение поверхности. Уравнения линии в пространстве

 

Уравнением поверхности в фиксированной системе координат называется та-кое уравнение с тремя переменными, которому удовлетворяют координаты любой точки данной поверхности и только они.

Из этого определения вытекает способ решения следующей простой задачи: выяснить, лежит ли данная точка на поверхности, определяемой заданным уравнением. Для решения задачи необходимо подставить ее координаты в данное уравнение, если получается числовое равенство, то точка лежит на поверхности, в противном случае точка поверхности не принадлежит.

Всякое уравнение с тремя переменными.Можно записать так:

(4.1)

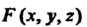
Где  — функция переменных.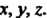

Из определения прямоугольных декартовых координат точки в пространстве (см. a I. T2) следует, что координатные плоскости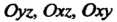Определяются соот

Ветственно уравнениями: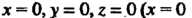- уравнение плоскостиИт. д.).

Линию в пространстве можно рассматривать как пересечение двух поверхностей, поэтому она определяется двумя уравнениями. Пусть- линия, по которой пересекаются поверхности, определяемые уравнениям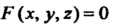иИ

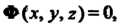Т. е. множество общих точек этих поверхностей, тогда координаты любой точки линии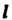Одновременно удовлетворяют обоим уравнениям:

(4.2)

Пример 4.1. Составить уравнение сферы радиусаС центром в точке Исходя из определения сферы как множества точек пространства, равноудаленных от данной точки (центра), для произвольной ее точки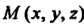> получаем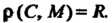Так как

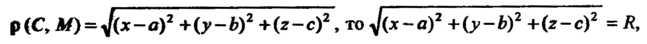
Шш

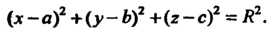
Для точки N, не лежащей на данной сфере, равенствоНе будет выпол

Нено, поэтому ее координаты не удовлетворяют уравнению (4.3). Следовательно, уравнение (4.3) является уравнением сферы радиуса R с центром в точке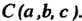

В частном случае, когда центр сферы находится в начале координат 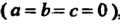, уравнение (4.3) принимает вид

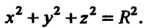(4.4)

Уравнение (4.4) называется каноническим уравнением сферы.

Пример 4.2. Уравнения

Определяют окружность радиусаЛежащую в плоскостиДействитель

Но, первое уравнение определяет сферу радиусаС центром в начале координат, второе уравнение - координатную плоскость

Пример 4.3. Ось Ох прямоугольной декартовой системы координат в пространстве определяется уравнениями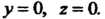

Действительно, уравнение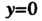Определяет координатную плоскость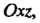А уравнение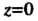- координатную плоскост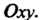ьОсьЯвляется линией пересечения координатных плоскосте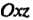йИ(см. рис. 1.13).

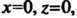Отметим, что осьИмеет уравненияА ось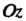- уравнения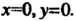

Поверхность, определяемая алгебраическим уравнениемСтепени относительно декартовых координат, называется поверхностью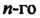Порядка. Сфера - поверхность второго порядка, так как ее уравнение (см. (4.3) и (4.4)) является уравнением второй степени относительно декартовых координат.

< Предыдущая		Следующая >