03.11. Аффинные координаты

 

Фиксируем некоторую точку О заданной плоскости и выберем два неколлинеар-ных вектора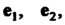Назовем эту точку началом координат, векторы-

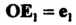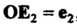Базисными. От точки О отложим векторыИ, проведем прямые,

Которым принадлежат векторы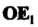И, фиксируем на них положительные

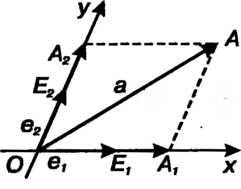
Направления, совпадающие с направлениями ИСоответственно, получим две координатные оси(рис. 3.15). Будем говорить, что построена общая декартова или аффинная системы координатПусть а

- любой вектор данной плоскости, отложим из точкиВектор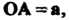Тогда по теореме 3.3

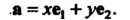(3.40)

Рис. 3.15  Числа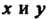Формулы (3.40) называются

Общими декартовыми или аффинными координатами вектора а в системе 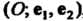, они также называются аффинными координатами точкиВ той

Же системе, т. е.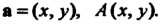

Так как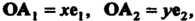То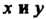- величины направленных отрезков

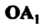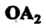ИКоординатных осей,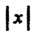- длина отрезка ОА1, измеренная с помощью масштабного отрезка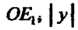- длина отрезка ОАг, измеренная с помощью масштабного отрезка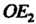. Другими словами, аффинными координатами точки(и вектора) называются числа х и у, определяемые формулами

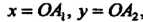
Где- величины направленных отрезковКоординатных

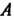Осей (— проекция точкиНа ось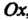, взятая параллельно оси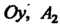- проек

Ция точкиНа ось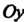, взятая параллельно оси; длины отрезков на каждой оси измеряются с помощью своего масштабного отрезка).

Аналогично вводится аффинная система координат в пространстве. Фиксируем начало координат - точку, базис - три некомпланарных вектора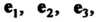 отложим из точкиВекторы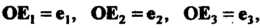Координатные оси

Если- любой вектор, то, отложив из точкиВекторПо

Теореме 3.5 получим

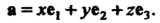(3-41)

Общими декартовыми или аффинными координатами вектора а (н точки А) называются числа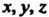В разложении (3.41).

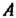Пусть- проекция точкиНа ось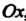, взятая параллельно координатной плоскости(определяемой векторами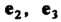), т. е. точка пересечения ос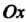иИ

Плоскости, проходящей через точку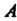И параллельной плоскости 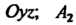проекция точки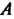На ось, взятая параллельно плоскости- проекция

Точки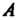На ось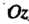, взятая параллельно плоскости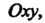Тогда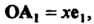

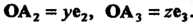
Следовательно,- проекции вектораНа координатные оси, т. е. величины направленных отрезков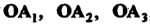, длины отрезков на каждой координатной оси измеряются с помощью своего масштабного отрезка (- на оси

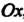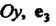,- на- на).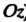

В частном случае векторы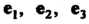Попарно перпендикулярны и имеют рав

Ные длины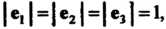Их называют ортами и обозначаютСистема

Координат называется прямоугольной.

Термин «орт» ввел О. Хевисайд (1892), обозначения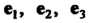- Г. Грассман

(1844),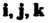- У. Гамильтон (1853).

Глава 4

ПОВЕРХНОСТИ И ЛИНИИ В ПРОСТРАНСТВЕ

< Предыдущая		Следующая >