03.10. Линейная зависимость векторов

 

ВекторыНазываются линейно зависимыми, если существуют дей

Ствительные числа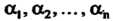Из которых по меньшей мере одно отлично от

Нуля, такие что

О.37)

В. противном случае (т. е. когда таких чисел не существует) векторы называются линейно независимыми; другими словами, векторы линейно независимы, если равенство (3.37) выполняется лишь при

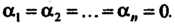(3.38)

Если один из векторов, например, является нулевым, то система Окажется линейно зависимой, так как равенство (3.37) будет выполнено при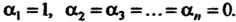Если часть векторов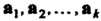Линейно зависима, то и вся система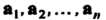Линейно зависима, поскольку из равенства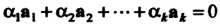Следует равенство" (3.37), в котором

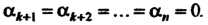
Теорема 3.1. ВекторыЛинейно зависимы тогда и

Только тогда, когда по меньшей мере один из них является линейной комбинацией остальных.

Теорема 3.2. Два вектора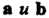Линейно зависимы тогда и только тогда, когда они коллинеарны.

Теорема 3.3. Есл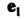иИ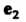— два неколлинеарных вектора некоторой плоскости, то любой третий вектор а той же плоскости можно единственным образом разложить по ним, т. е. представить в виде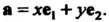

Теорема 3.4. Три вектора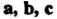Линейно зависимы тогда и только тогда, когда они компланарны.

Теорема 3.5. Если векторыНекомпланарны, то любой вектор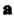

Можно единственным образом разложить по ним, т. е.

Теорема 3.6. Всякие четыре вектора линейно зависимы.

Любая упорядоченная система трех линейно независимых (т. е. некомпланарных) векторовНазывается базисом. Согласно теореме 3.5, всякий вектор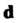 можно разложить по базису, т. е. представить в виде

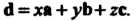(3.39)

Числа х, у, г называют координатами вектораВ базисе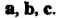 Пр и мер 3.11. Образуют ли базис векторы

?

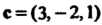Так как

Т. е. смешанное произведение отлично от нуля, то векторы некомпланарны. Значит, они линейно независимы и образуют базис.

Пример 3.12. Даны векторы

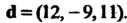Доказать, что векторы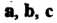Образуют базис и найти координаты

Вектора d в этом базисе.

Поскольку

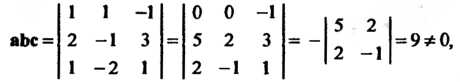
То векторы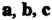Линейно независимы (некомпланарны) и образуют базис. Вектор Можно представить в виде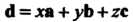(см. формулу (3.39)). Это равенство

Равносильно следующим равенствам:

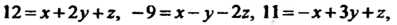
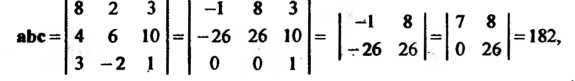
Так как равные векторы имеют равные координаты и координаты линейной координации векторов равны соответствующим линейным комбинациям одноименных координат (см. п. 3.5). Решив полученную систему уравнений, найдем Итак,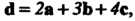ВекторВ данном базисе имеет координаты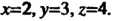

< Предыдущая		Следующая >