03.09. Смешанное произведение трех векторов

 

Пусть даны три вектора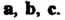Вектор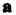Умножим векторно на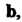Векторное

Произведение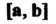Умножим скалярно на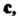В результате получаем число, кото

Рое называют векторно-скалярным произведением или смешанным произведением 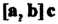Трех векторов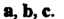

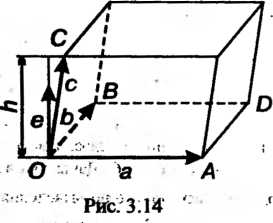
Смешанное произведение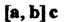Трех некомпланарных векторов равно объе

Му параллелепипеда, построенного на векторах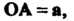

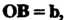
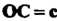
(рис. 3.14), взятому со знаком плюс, если тройка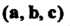— правая, со знаком

Минус, когда эта тройка — левая:

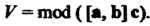(3.30)

Векторы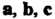Компланарны тогда и только тогда, когда их смешанное произведение равно нулю, т. е.

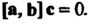
Смешанное произведение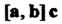И

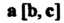Обозначают через

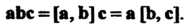
(3.31)

(3.32)

 

Если поменять местами два вектора, то смешанное произведение изменит лишь знак. Для трех векторов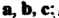

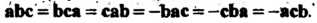
Смешанное произведение трех векторов

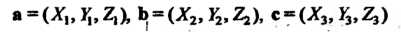
Определяется формулой

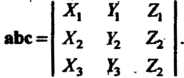(3.33)

Из формул (3.30) н (3.33) следует, что объем параллелепипеда, построенного

Объем треугольной пирамиды с вершинами в точках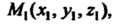

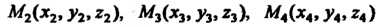Определяется формулой

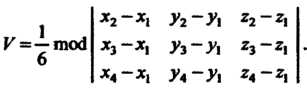(3.35)

Необходимое и достаточное условие компланарности трех векторов (3.32) выражается равенством

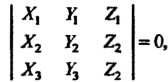(3.36)

Которое следует из равенств (3.31), (3.33).

Пример 3.8. Найти объем параллелепипеда, построенного на векторах

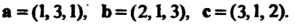
На векторах (3.32), вычисляется по формуле

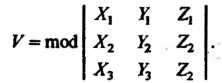
(3.34)

 

По формуле (3.34) получаем

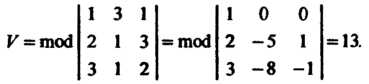
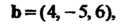
Пример 3.9. Доказать, что векторы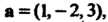 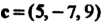Компланарны.

Так как

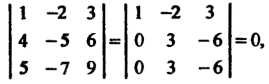
Т. е. выполнено условие (3.36), то данные векторы компланарны.

Пр им ер 3.10. Вычислить объем треугольной пирамиды, вершины которой находятся в точках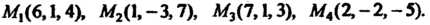

В соответствии с формулой (3.35) находим

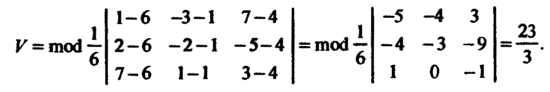
< Предыдущая		Следующая >