03.08. Векторное произведение двух векторов

 

Векторным произведением вектора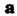На векторНазывается третий вектор, обозначаемый символомИ удовлетворяющий условиям:

1)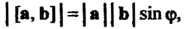Где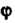- угол между векторами;

2)  вектор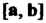Перпендикулярен каждому из векторов;

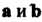3)  тройка векторовИмеет ту же ориентацию, что и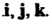

Для векторного произведения применяют и другие обозначения, например

Замечание. Если пользоваться только правыми системами координат, то условие 3) можно заменить другим - тройкаЯвляется правой.

Понятие векторного произведения возникло в механике. Если вектор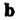Изображает силу, приложенную в точкеТоВыражает момент силыОтносительно точки

Из условия 1) следует, что модуль векторного произведения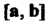Равен площадиПараллело

Грамма, построенного на векторах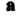И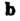 (рис. 3.13), т. е.

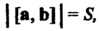(3-24)

Поэтому

Где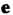- единичный вектор направления вектора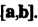

Равенство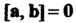Выражает необходимое и

Достаточное условие коллинеарности двух векторов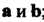; в частности, для любого вектора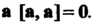

Векторное произведение двух векторов обладает свойствами:

1)  антиперестановочности множителей

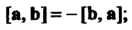
2)  сочетательности относительно скалярного множителя

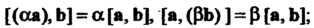
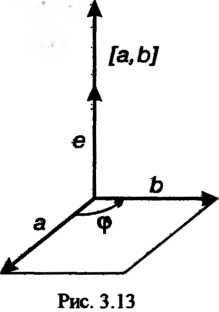
3)  распределительности относительно сложения

Векторное произведение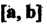Двух векторов

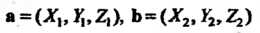
(3.25)

Выражается формулой

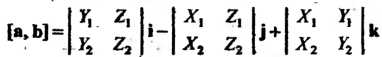
(3.26)

Эту формулу можно представить через символический определитель третьего порядка

(3.27)

 

Замечание. Составим матрицу из координат векторов а и b

Координаты векторного произведения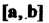Равны минорам второго порядка

Этой матрицы, полученным путем поочередного вычеркивания первого, второго и третьего столбцов, причем второй минор нужно взять со знаком минус.

Площадь параллелограмма, построенного на векторах (3.25), вычисляется по формуле

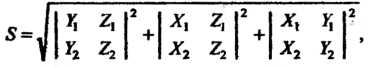(3.28)

Которая следует из (3.11) и (3.24).

Площадь треугольника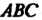Определяется формулой

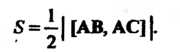
(3.29)

Формула (3.29) следует из (3.24), так как площадь треугольникаСоставляет половину площади параллелограмма, построенного на векторах

Пример 3.6. Даны два вектора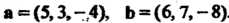. Найти ко

Ординаты векторного произведения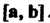 Поформуле (3.27) получаем

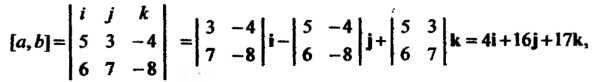
Пример 3.7. Вершины треугольника находятся в точках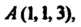 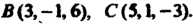Вычислить его площадь.

 

С помощью формул (3.15) находим координаты векторовИ

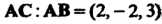,.‘Гак как

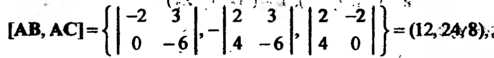
То

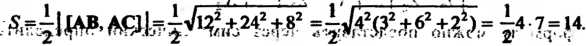
< Предыдущая		Следующая >