03.07. Правые и левые тройки векторов. Правые и левые системы координат
Три некомпланарных вектора
Взятых в указанном
Порядке (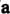
- первый вектор,
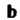- второй,
- третий) и приложенных в одной точке (рис. 3.12, а, б), называют тройкой векторов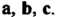
Будем смотреть с конца
Вектора с на плоскость, определяемую векторами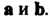
Если кратчайший поворот
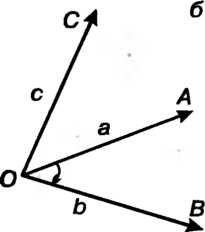
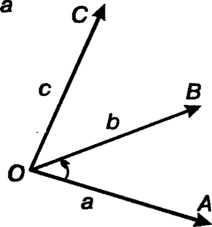
Рис. 3.12
От вектора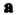
К вектору
Совершается против часовой стрелки, то тройка векторов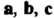 
Называется правой1 (рис. 3.12, а), если указанный поворот совершается по часовой стрелке, тройка
Называется левой (рис. 3.12, б).
Две тройки, обе правые или обе левые, называются тройками одной ориентации; если одна тройка является правой, а другая левой, то они называются тройками различной ориентации.
При круговой перестановке векторе® (первый заменяется вторым, второй - третьим, третий - первым, рис. 3.12, е) ориентация тройки не меняется (см. рис. 3.12, а, б).
Бели поменять местами два вектора, то ориентация тройки меняется, например если
— правая тройка, то тройка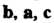
(тех же векторов, взятых в порядке
) будет левой.
Прямоугольная декартова система координат называется правой, если тройка базисных векторов
Правая; если эта тройка левая, то система координат называется левой.
| < Предыдущая | Следующая > |
|---|
