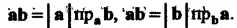03.06. Скалярное произведение двух векторов

 

Скалярным произведением двух векторов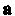ЙНазывается число, равное произведению их длин на косинус угла мещу римй. ;Если обозначить скалярное произведение через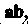То  ,

°  ...............:':°т : V

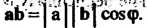
Такюис(рйс. 3.11), то равенство (3.18) можно

Представить в двух видах:i - '¦¦)  у-i, . v.

' ,i

Понятие скалярного произведения возникло в механике. Если вектор а изображает силу, точка приложения которой перемещается из начала в конец вектора

Ь, то работа w указанной силы определяется равенством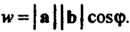

Скалярным квадратом вектора а называется скалярное произведение вектора а на себя:

Т. е. скалярный квадрат вектора равен квадрату его длины.

Векторы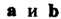Перпендикулярны тогда и

Только тогда, когда

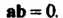(3.19)

Скалярное произведение обладает свойствами:

1)  переместительности (коммутативности)

2)  сочетательности (ассоциативности) относительно числового множителя

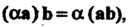
3)  распределительности (дистрибутивности) относительно суммы векторов  Скалярное произведение двух векторов

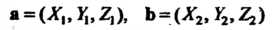(3.20)

Выражается формулой

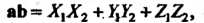(3.21)

Т. е. скалярное произведение двух векторов равно сумме произведений одноименных координат.

Замечание. Если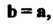То формула (3.21) принимает вид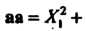

. Поскольку

Косинус угла между векторами (3.20) определяется формулой

(3.22)

Необходимое и достаточное условие перпендикулярности двух векторов (3.20) выражается равенством

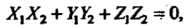(3.23)

Оно следует из формул (3.19) и (3.21).

Если осьОбразует с координатными осями углыСоответственно, то

Проекция вектораНа эту ось определяется равенством

Пример 3.4. Даны два вектораНайти

Угол между ними.

По формуле (3.22) получаем

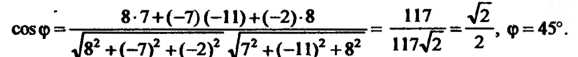
Пример 3.5. Доказать, что векторы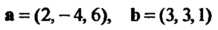Пер

Пендикулярны.

По формуле (3.21) находим: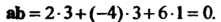Так как выполнено ус

Ловие (3.19), то векторы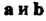Перпендикулярны.

< Предыдущая		Следующая >