03.05. Переход от векторных соотношений к координатным

 

Если даны векторы (т. е. известны их координаты) и указаны определенные соотношения между ними, то они равносильны аналогичным числовым соотношениям между координатами.

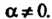Координаты произведения вектора на число. Пусть дан вектор И числоКоординаты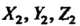Вектора

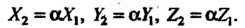(3.14)

Отметим, что равенства (3.14) выражают необходимое и достаточное условие коллинеарности двух векторов:. Если ни одно из

ЧиселНе равно нулю, то эти равенства можно записать так:

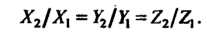
Векторы коллинеарны тогда и только тогда, когда пропорциональны их одноименные координаты.

Координаты суммы (разности) двух векторов. Пусть даны два вектора

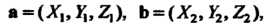Тогда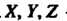- координаты вектора суммы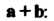

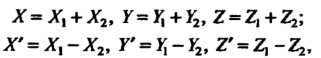
Где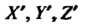— координаты разности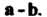

Координаты вектора, заданного двумя точками. Начало вектораНа

Ходится в точке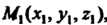Конец - в точке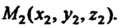Выражение для

Его координат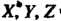Через координаты точек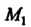И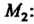

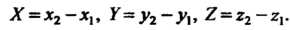(3.15)

Координаты линейной комбинации векторов. Заданы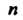Векторов

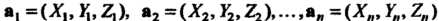И их линейная комбинация

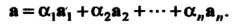
КоординатыВектора а определяются формулами

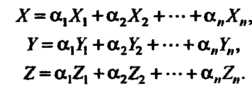
Деление отрезка в данном отношении. Даны две точки в пространстве

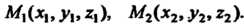Координаты точки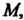Делящей отрезокВ

Отношении I: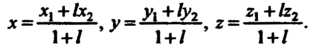

В частности, координаты середины отрезка определяются формулами

Преобразование декартовых прямоугольных координат при параллельном переносе.

Рассмотрим две декартовы прямоугольные системы координат с одним и тем же масштабным отрезком й одинаковыми направлениями одноименных координатных осей (рйс. ЗЛО). Начало новой системы координат находится в точке 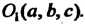Пусть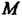— произвольная точка пространства,Ее координаты в старой системе,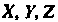- в новой, тогда

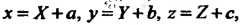
Или

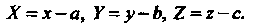(3-17)

П р и м е р 3.2. Даны две точки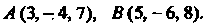Найти координа

Ты вектора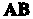И координаты точки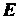— середины отрезка 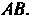По формулам (3.15) и (3.16) соответственно получаем

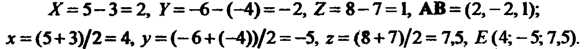
Пример 3.3. Даны четыре точки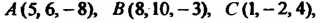

Коллинеарны ли векторыИ?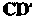

Так как

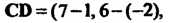
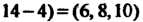И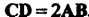, т. е. выполнено равенство (3.1), то векторыИ

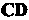Коллинеарны.

< Предыдущая		Следующая >