03.04. Декартовы прямоугольные координаты вектора в пространстве. Длина вектора. Направляющие косинусы вектора
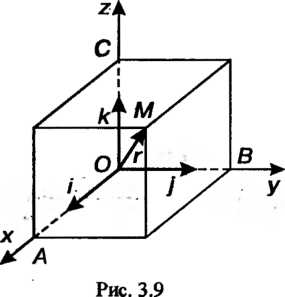
Рассмотрим в пространстве декартову прямоугольную систему координат. Ра-диусом-вектором точки Называется вектор
Называется вектор Точка приложения которого
Точка приложения которого
Совпадает с началом координат, а конец находится в точке М (рис. 3.9).
Декартовыми прямоугольными координатами Вектора
Вектора Называются его
Называются его
Проекции на координатные оси

Каждая из записей


(3.8)
(3.9)
Означает что вектор г имеет координаты
Если - декартовы прямоугольные координаты точки
- декартовы прямоугольные координаты точки ,то
,то
Т. е. координаты радиуса-вектора равны координатам точки
равны координатам точки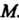
Введем в рассмотрение единичные векторы Координатных осей (их
Координатных осей (их
Называют ортами) и векторы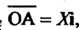
 Где
Где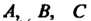 -
-
Вершины прямоугольного параллелепипеда, для которого Является диагональю
Является диагональю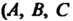 - проекции точки М на координатные оси;
- проекции точки М на координатные оси;
 - проекции вектора на координатные оси). По определению суммы
- проекции вектора на координатные оси). По определению суммы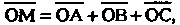 Поэтому
Поэтому
 (3.10)
(3.10)
Формула (3.10) выражает разложение вектора г по базисным векторам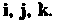 Векторы стоящие в правой части формулы (3.10), называются составляющими или компонентами вектора г.
Векторы стоящие в правой части формулы (3.10), называются составляющими или компонентами вектора г.
На основании теоремы о квадрате диагонали прямоугольного параллелепипеда получаем формулу, выражающую длину вектора (3.9) или (3.10) через его координаты:
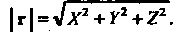 (3.11)
(3.11)
Из равенства (3.3) следует, что равные векторы имеют равные координаты, поэтому координаты вектора не зависят от точки его приложения. Координатами любого вектора называются его проекции на координатные оси.
Направляющими косинусами вектора называются косинусы углов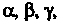 Обра
Обра
Зуемых им с координатными осями.
Принимая во внимание формулу (3.2), для вектора (3.9) получаем
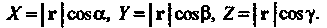 (3.12)
(3.12)
Из равенств (3.11) и (3.12) следуют формулы для направляющих, косинусов вектора г:
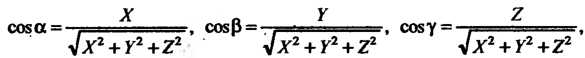 (3-13)
(3-13)
Откуда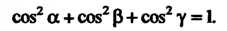
Из формулы (3.12) следует, что координаты единичного вектора равны его направляющим косинусам; т. е.
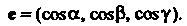
Пример 3.1. Дан вектор Найти его длину и единичный
Найти его длину и единичный
Ректор Направления вектора
Направления вектора
По формуле (3.11) находим длину вектора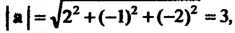 А по
А по
Формулам (3.13) - его направляющие косинусы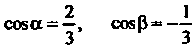
| < Предыдущая | Следующая > |
|---|