03.03. Проекция вектора на ось
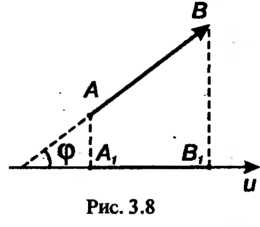
В пространстве заданы вектор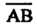 И ось
И ось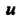 (рис. 3.8). Пусть
(рис. 3.8). Пусть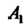 - проекция точки
- проекция точки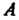 На ось
На ось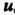 ,
,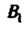 - проекция точки
- проекция точки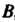 , т. е. основания перпендикуляров, опущенных из данных точек на эту ось.
, т. е. основания перпендикуляров, опущенных из данных точек на эту ось.
Проекцией вектора на ось Называется величина направленного отрезка
Называется величина направленного отрезка
(вектора) оси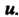 Проекция вектора на ось и обозначается через
Проекция вектора на ось и обозначается через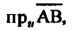 Т. е.
Т. е.
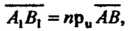 Вычисляется по формуле
Вычисляется по формуле
(3.2)
Из равенства (3.2) следует, что если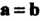 То
То
(3.3)
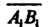

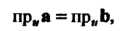
Т. е. равные векторы имеют равные проекции (на одну и ту же ось).
(3.1)

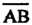
Где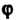 — угол между вектором и осью
— угол между вектором и осью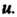
Проекция вектора на ось обладает следующими свойствами:
(3-4)
(3.5)
 (3.6)
(3.6)
Если - произвольная конечная система векторов;
- произвольная конечная система векторов;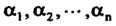 -
-
Произвольная система действительных чисел, то вектор
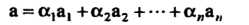
Называется линейной комбинацией векторов этой системы.
Из равенств (3.4) — (3.6) следует, что
 (3.7)
(3.7)
| < Предыдущая | Следующая > |
|---|